Łańcuchy Markowa są, obok Wartości Shapleya, jedną z często wykorzystywanych metod algorytmicznego modelowania atrybucji. Z tego artykułu dowiesz się, na czym polegają oraz jakie są ich zalety i wady w kontekście wykorzystania w modelowaniu atrybucji.
Poprzedni Artykuł (cz. 10): Wartość Shapleya
Czym jest łańcuch Markowa?
Łańcuch Markowa to proces losowy, w którym prawdopodobieństwo każdego zdarzenia zależy jedynie od zdarzenia poprzedniego.
Przykładem łańcucha Markowa może być następujący proces:
Wyjeżdżam na tygodniowy urlop. To, czy podczas tego urlopu będę uprawiać kontuzjogenny sport, czy oddawać się relaksowi, zależy od tego, gdzie będę spędzać wakacje. Ryzyko wypadku podczas relaksu jest znikome, natomiast sport wiąże się z 1/10 prawdopodobieństwem wypadku:
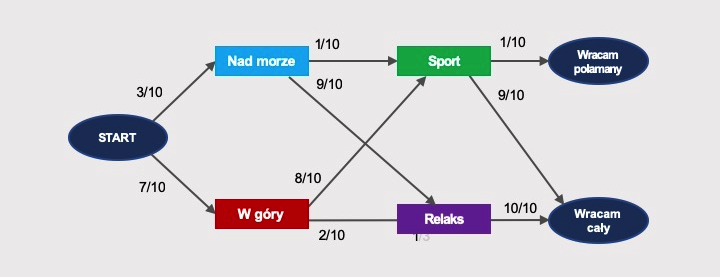
Z grafu można odczytać, że wypadek może zdarzyć się zarówno przy wyjeździe nad morze, jak i w góry.
Prawdopodobieństwo, że w dane wakacje wyjadę w góry ORAZ ulegnę tam wypadkowi, czyli przejścia START > W góry > Sport > Wracam połamany, wynosi:
P(góry) = 7/10 × 8/10 × 1/10 = 56/1000 = 5,6%
Z kolei szansa, że w te wakacje wyjadę nad morze ORAZ ulegnę tam wypadkowi, czyli przejścia START > Nad morze > Sport > Wracam połamany, wynosi:
P(morze) = 3/10 × 1/10 × 1/10 = 3/1000 = 0,3%
Innej możliwości dojścia do wypadku nie ma. Łączne prawdopodobieństwo wypadku wynosi więc:
P = P(góry) + P(morze) = 5,6% + 0,3% = 5,9%
Tłumaczy to, dlaczego przy trzech wyjazdach na urlop w roku, co 5-6 lat wracam w gipsie.
Łańcuch Markowa dla ścieżek konwersji
W jaki sposób możemy zastosować łańcuchy Markowa do analizy ścieżek wielokanałowych?
Wyobraźmy sobie, że w naszych działaniach marketingowych mamy tylko cztery ścieżki, z których dwie doprowadziły do konwersji. Współczynnik konwersji wynosi więc 50% (tak, to dużo, ale na takich liczbach łatwiej będzie zrozumieć obliczenia).

Ścieżki te możemy zilustrować w postaci poniższego grafu:
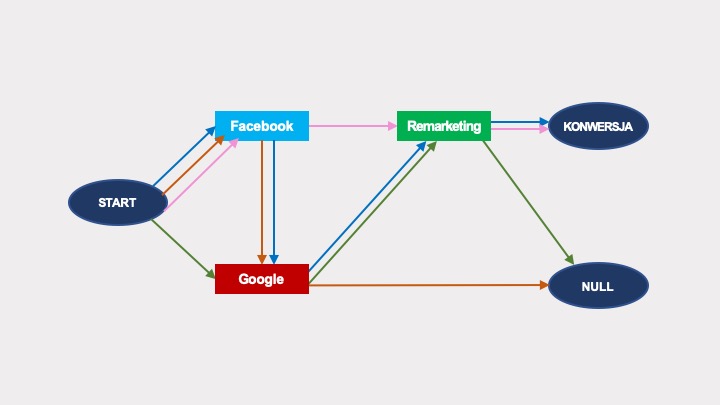
Dla zwiększenia czytelności, zamiast kilku strzałek zastosujemy jedną ze wskazaniem liczby możliwych przejść po danym łuku. Liczba ta, po podzieleniu przez liczbę wszystkich łuków wychodzących z danego węzła, da prawdopodobieństwo przejścia między węzłami grafu:
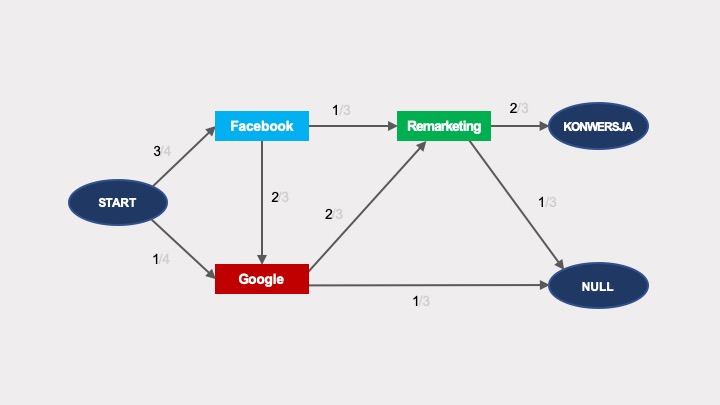
Zobaczmy teraz, jakie prawdopodobieństwo konwersji wynika z tego grafu.
W tym celu musimy obliczyć sumę prawdopodobieństw dojścia do konwersji dla wszystkich możliwych sposobów przejścia od węzła START do węzła KONWERSJA. W tym przypadku są trzy takie sposoby, zaznaczone na grafie różnymi kolorami.
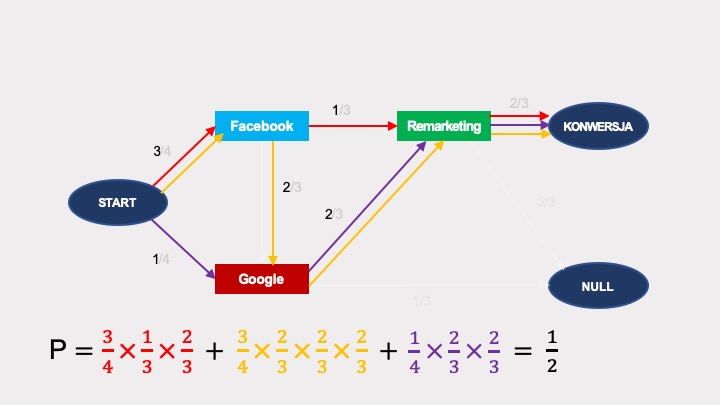
Łączne prawdopodobieństwo wynosi 1/2, czyli 50%, co zgadza się ze współczynnikiem konwersji analizowanych ścieżek.
Zauważ, że liczba możliwych przejść w grafie łańcucha Markowa jest różna od liczby ścieżek prowadzących do konwersji.
Atrybucja w łańcuchach Markowa
Modelowanie atrybucji z wykorzystaniem łańcuchów Markowa opiera się o analizę, na ile usunięcie danego węzła (danego kanału marketingowego) z grafu wpłynie na prawdopodobieństwo konwersji.
Zobaczmy, co się stanie, jeśli usuniemy Facebook.
Łuki (strzałki) wychodzące z tego węzła przestaną istnieć. W związku z tym, w takim okrojonym grafie jest tylko jeden sposób dojścia do konwersji (zaznaczony na czerwono). Jego prawdopodobieństwo wynosi 1/9:
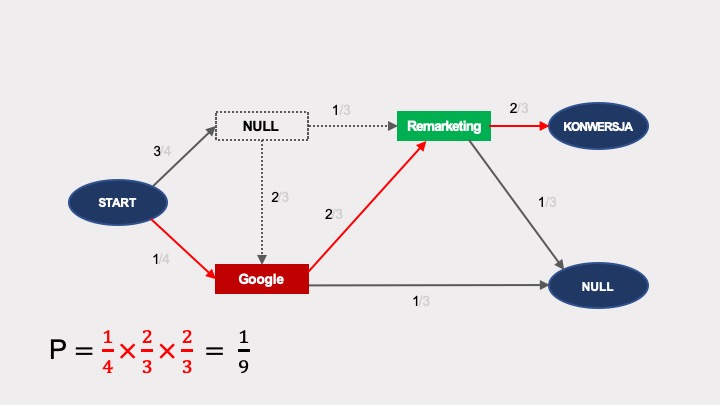
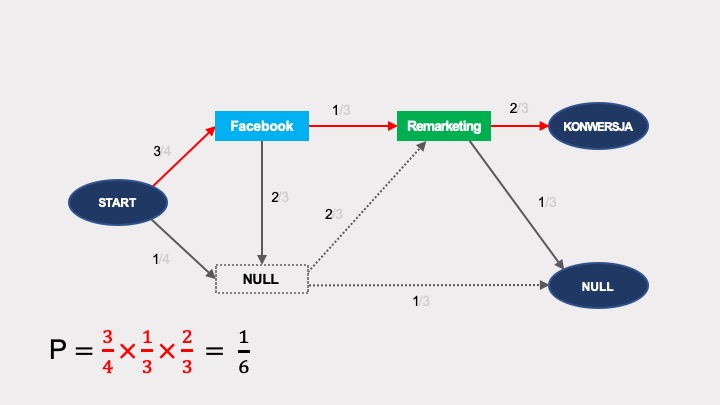
Podobne obliczenia dla Google’a wykażą, że po usunięciu tego węzła, prawdopodobieństwo konwersji w grafie bez Google’a wynosi 1/6.
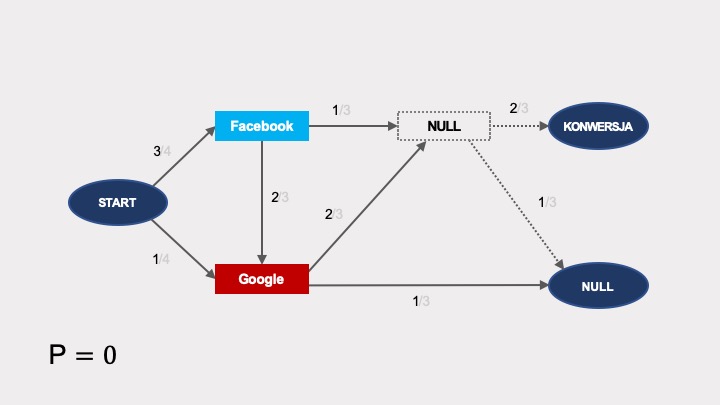
Usunięcie remarketingu z grafu powoduje, że w grafie nie ma możliwości dojścia do konwersji. Prawdopodobieństwo konwersji w grafie bez remarketingu wynosi zero:
Analiza atrybucji wymaga obliczenia efektu usunięcia danego węzła. Oblicza się go według formuły:
Efekt usunięciai = 1 – (Pz udziałem i / Pbez udziału i)
gdzie P oznacza prawdopodobieństwo konwersji.
Efekt usunięcia określa, jaką część konwersji utracimy, jeśli usuniemy dany kanał. Efekty usunięcia nie sumują się do 100%, więc aby obliczyć udział w wyniku, efekty usunięcia trzeba znormalizować, zmniejszając je proporcjonalnie tak, by łącznie sumowały się do jedności (do 100%).
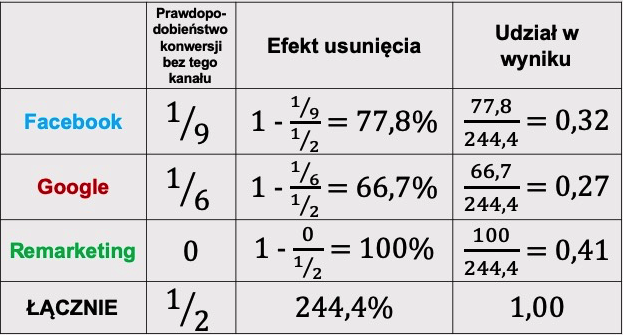
Oczywiście, aby obliczyć konwersje przypisane do danego kanału, trzeba udział w wyniku pomnożyć przez łączną liczbę konwersji.
W naszym przypadku mamy tylko 2 konwersje (dwie ścieżki, każda prowadzi do jednej konwersji), dlatego atrybucja w modelu wykorzystującym łańcuch Markowa w tym przypadku będzie wyglądała następująco:
| Kanał | Udział w wyniku | Przypisane konwersje |
| 0,32 | 0,32 x 2 = 0,64 | |
| 0,27 | 0,27 x 2 = 0,54 | |
| Remarketing | 0,41 | 0,41 x 2 = 0,82 |
| Łącznie | 1,00 | 2,00 |
Brak ścieżek niekonwertujących
W raportach Google Analytics nie są dostępne bezpośrednio raporty dotyczące ścieżek niekonwertujących.
Dane o ścieżkach niekonwertujących uzyskać tworząc konwersję w postaci dowolnej wizyty na stronie lub uzyskać dane o wizytach wykorzystując segmenty konwersji, bądź – najlepiej – wykorzystać inne narzędzie do śledzenia interakcji i konwersji, np. Campaign Manager (Google Marketing Platform).
Typowy raport ścieżek konwersji zawiera tylko ścieżki prowadzące do konwersji:
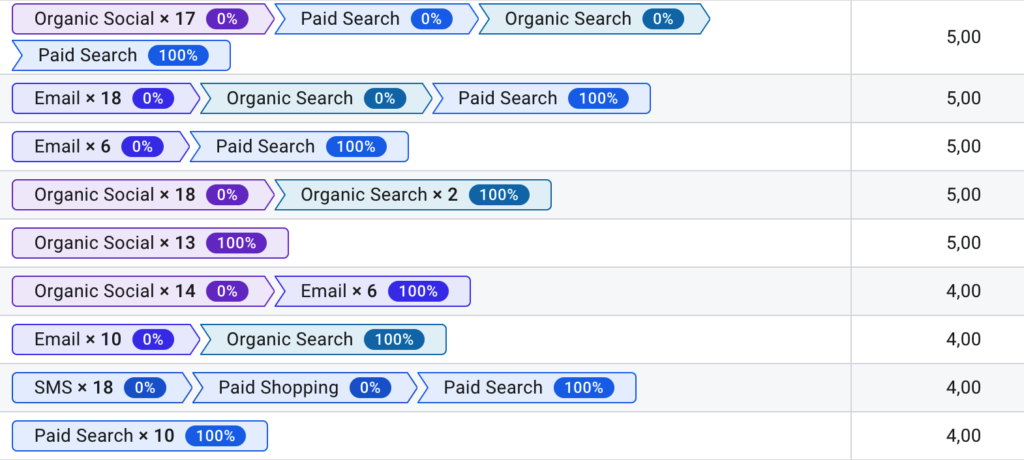
Łańcuchy Markowa można również tworzyć dla danych zawierających wyłącznie ścieżki konwertujące.
Ścieżki konwertujące w omawianym wcześniej przykładzie wyglądają następująco:
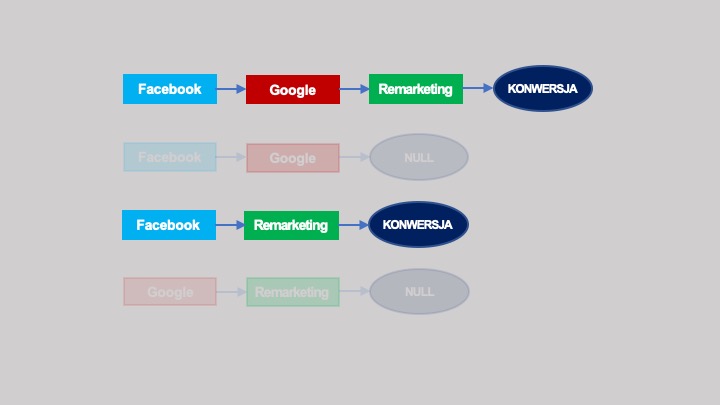
Po przekształceniu w graf:

W takim łańcuchu prawdopodobieństwo konwersji wynosi 1, ponieważ wszystkie ścieżki do niej prowadzą.
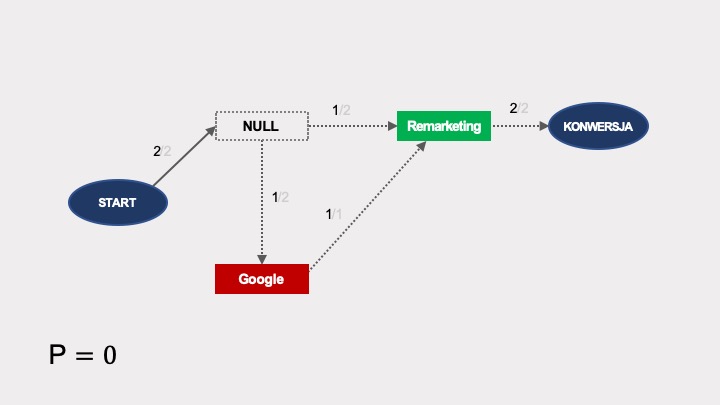
Podobnie jak w poprzednich przykładach, obliczmy efekt usunięcia dla poszczególnych kanałów. Prawdopodobieństwo konwersji po usunięciu Facebooka jest zerowe:
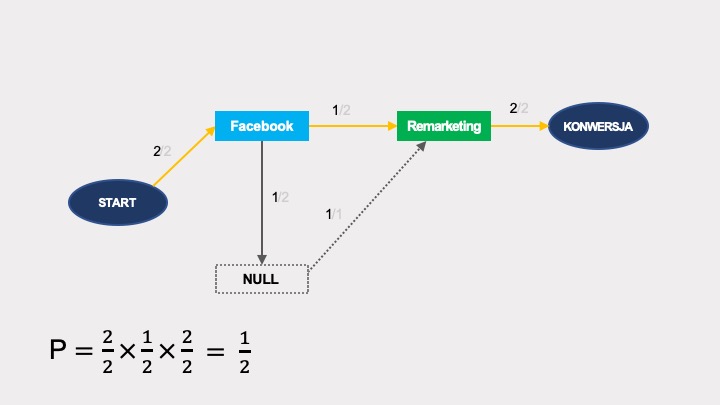
Przy usunięciu Google’a, prawdopodobieństwo konwersji wynosi 1/2:
Przy usunięciu remarketingu prawdopodobieństwo konwersji wynosi zero:
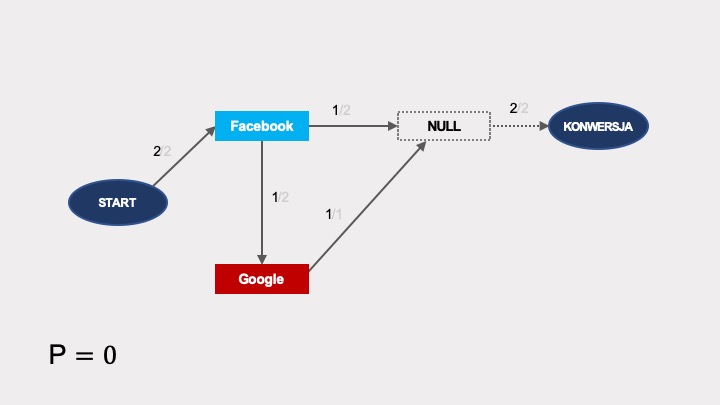
W ten sposób możemy obliczyć udziały w wyniku dla poszczególnych kanałów:

Ciekawostką jest, że w tym przypadku model wykorzystujący łańcuchy Markowa sprowadził się do tej samej atrybucji, co model liniowy.
Nie jest to jednak reguła, tak jak w przypadku wartości Shapleya liczonej bez uwzględniania ścieżek niekonwertujących. Zbieżność z modelem liniowym będzie dotyczyła tylko mniej skomplikowanych grafów.
Przykładow, wynik będzie inny przypadku ścieżek takich, jak poniżej:
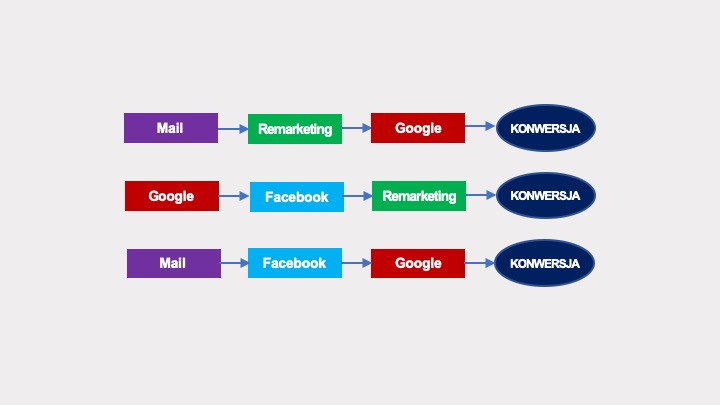
Zbudowany na ich bazie graf będzie nieco bardziej rozbudowany, ale to, co go odróżnia od poprzedniego, to zapętlenia w grafie (zaznaczone na żółto).
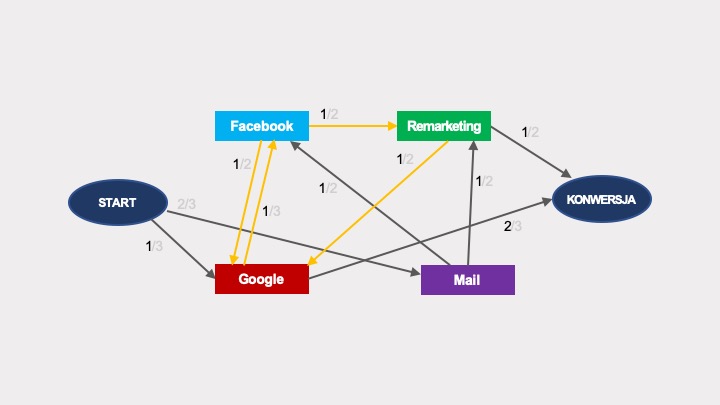
Pętle
Pętle w łańcuchach Markowa stanowią szczególną sytuację, która istotnie komplikuje obliczenia prawdopodobieństw przejścia po grafie. Komplikacja wynika z tego, że możliwych przejść po grafie jest nieskończenie wiele, bo do każdej z pętli można wejść dowolnie wiele razy.
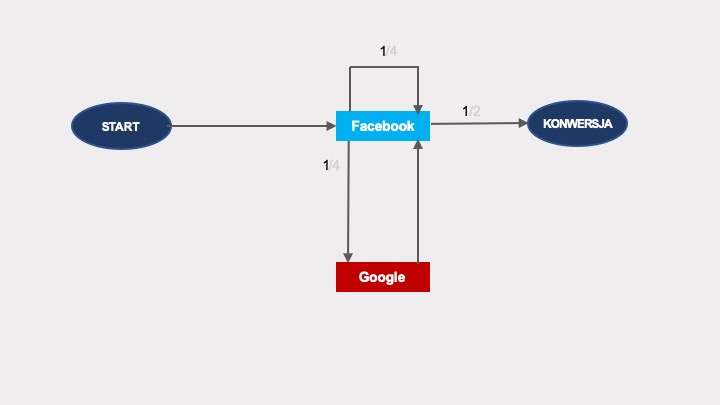
Zobaczmy, jak to wygląda na przykładzie najprostszych pętli. Mamy dwie ścieżki prowadzące do konwersji:
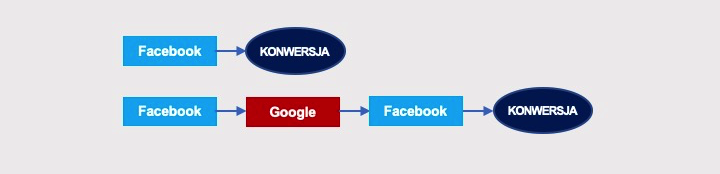
Graf łańcucha Markowa dla tych interakcji wygląda następująco:
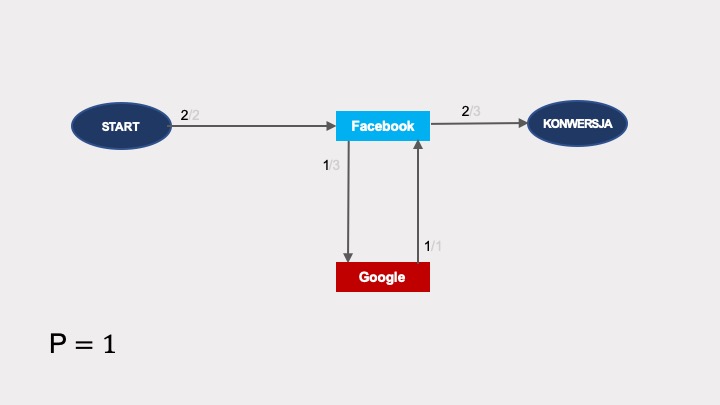
Prawdopodobieństwo konwersji wynosi w nim 1. Zobaczmy, w jaki sposób można dojść do konwersji po grafie. Pierwsze przejście nie zawiera żadnej pętli i reprezentuje ścieżkę START > Facebook > KONWERSJA. Jego prawdopodobieństwo wynosi 2/2 × 2/3:

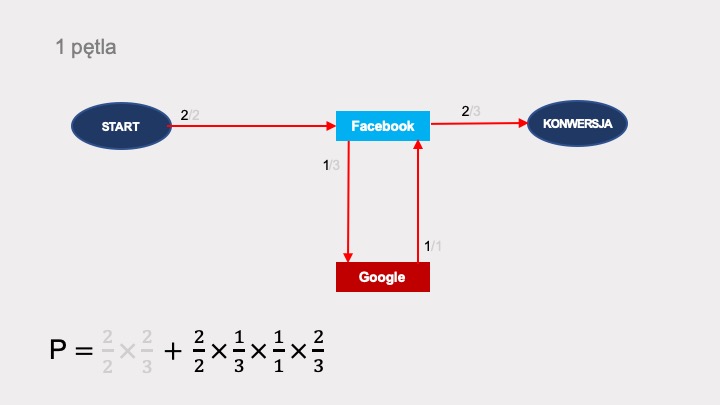
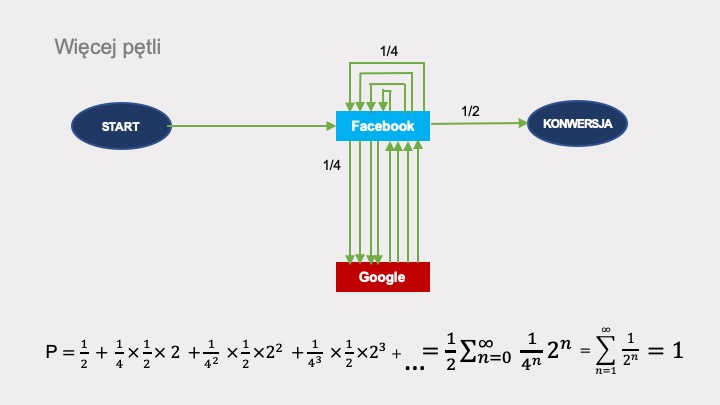
Do konwersji można też dojść wykonując pętlę, przechodząc przez węzeł Google. Po jej dodaniu, prawdopodobieństwo się zwiększa o kolejny składnik:
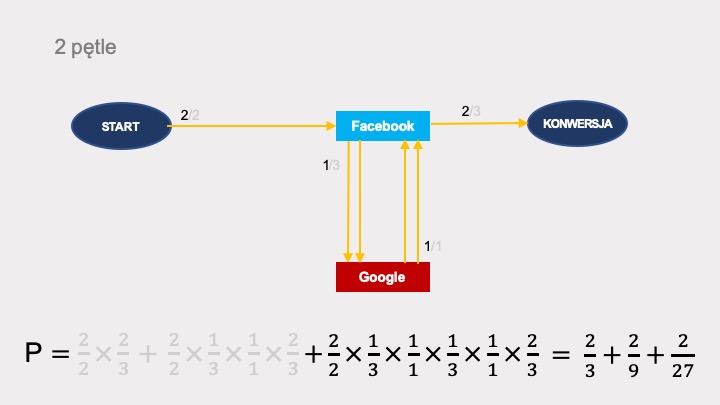
Kolejna pętla to kolejny składnik prawdopodobieństwa konwersji:
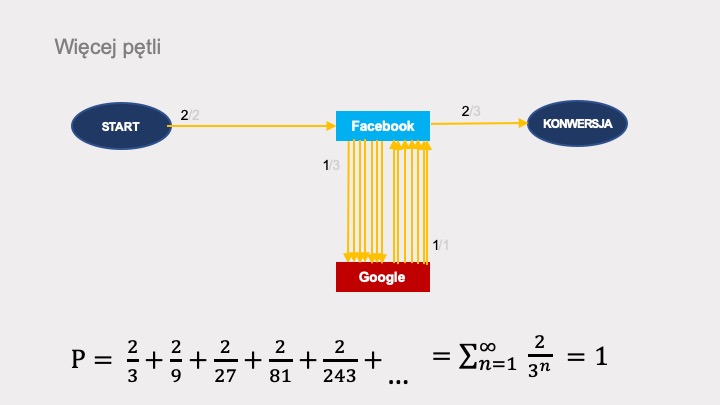
Po dodaniu kolejnych pętli, szereg prawdopodobieństw będzie zbliżał się do jedności.
Sytuacja komplikuje się jeszcze bardziej, gdy pętli jest więcej niż jedna. W przypadku takich ścieżek:
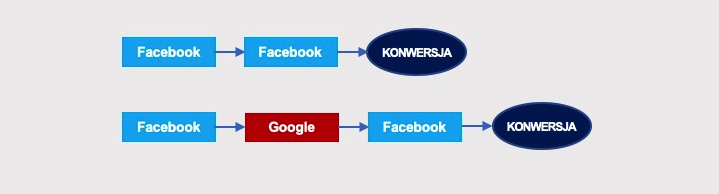
…graf będzie wyglądał następująco:
Obliczenia w tym wypadku będą jeszcze bardziej złożone, ponieważ możliwości przejścia po grafie dla jednej pętli są dwie, dla dwóch pętli – cztery, dla trzech pętli – osiem, dla n pętli jest 2n możliwości:
W przypadku bardziej rozbudowanych grafów będzie to jeszcze bardziej skomplikowane. Jest oczywiste, że obliczanie łańcuchów Markowa musi się odbywać metodami numerycznymi.
Powtórzenia interakcji
Jeżeli w przykładowym grafie:
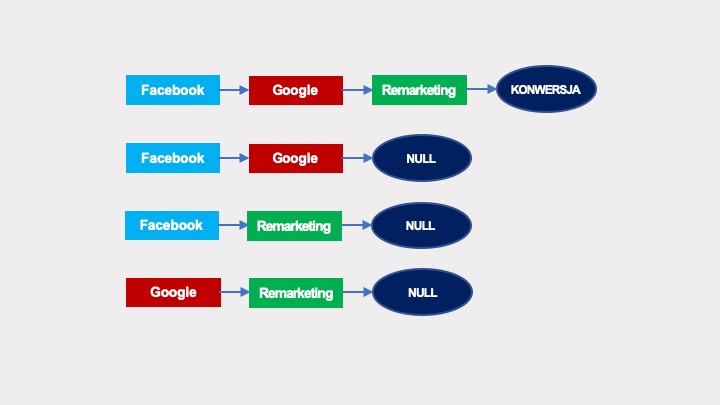
… na jednej ze ścieżek pojawiłoby się powtórzenie interakcji:
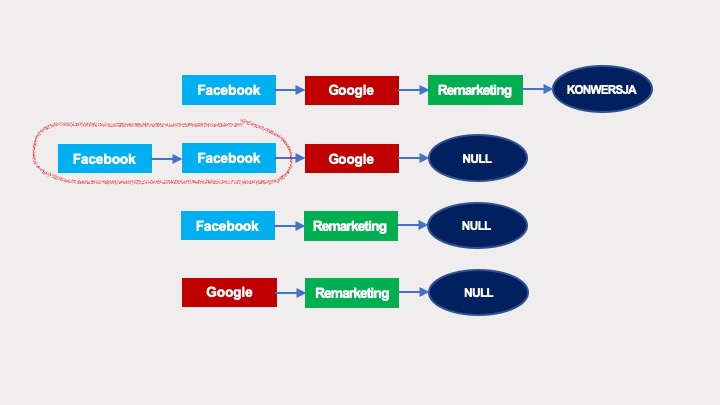
… to modyfikacja grafu wyglądałaby tak, jak poniżej. Pierwszy graf jest bez powtórzenia interakcji z Facebookiem, pod nim ten sam graf zawierający pętle reprezentujące powtórzenie:
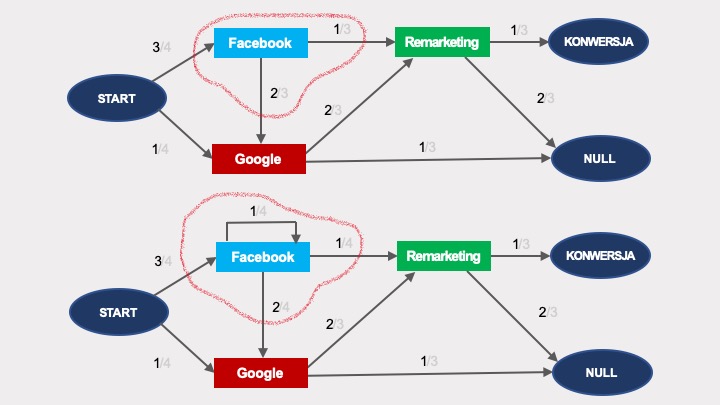
Obliczenie takiej pętli jest trywialne. Zauważmy, że efekt usunięcia węzła nie zawierającego powtórzenia (u góry) będzie dokładnie taki sam, jak usunięcie takiego węzła z powtórzeniem (poniżej):
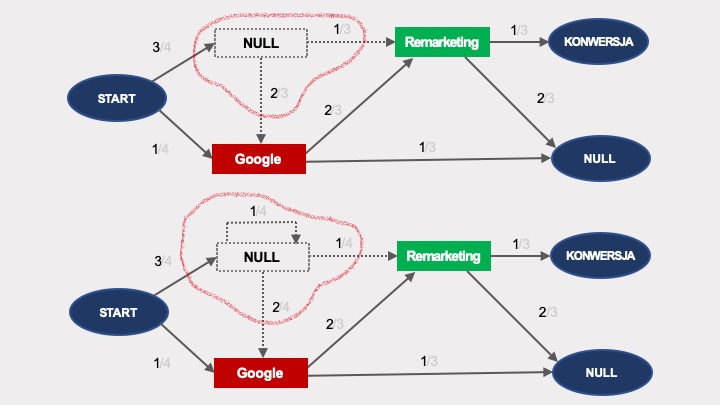
Dlatego z punktu widzenia obliczania prawdopodobieństw przejścia w grafie, powtórzenia nic nie zmieniają i takie grafy są równoważne.
Innymi słowy, jeśli na ścieżce znajdują się powtórzenia, np. Facebook > Facebook > Google > Remarketing > Remarketing, to taka ścieżka jest równoważna ścieżce bez powtórzeń (Facebook > Google > Remarketing) i można je po prostu zignorować (zastąpić powtórzenia pojedynczą interakcją).
Łańcuchy Markowa wyższego rzędu
Zgodnie z definicją, w łańcuchach Markowa prawdopodobieństwo każdego zdarzenia zależy jedynie od zdarzenia poprzedniego. Oznacza to, że węzły klasycznego łańcucha Markowa “nie mają pamięci”.
Co to oznacza w praktyce? Spójrz na poniższy graf. Prawdopodobieństwo konwersji po interakcji z Remarketingiem jest 2/3, niezależnie od tego, czy wcześniejsza wizyta była z Facebooka, czy z Google’a:
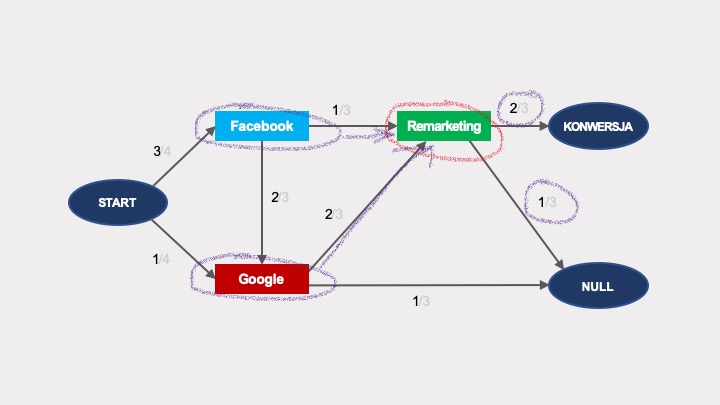
Wiemy, że w rzeczywistości nie jest to prawda.
Skuteczność remarketingu będzie diametralnie inna w zależności od tego, skąd przyszedł dany użytkownik, czy będzie to osoba, która wcześniej szukała Twojego produktu w Google, czy ktoś, kogo zaciekawił Twój post na Facebooku.
Tę kwestię rozwiązują łańcuchy Markowa wyższego rzędu. W przypadku łańcuchów drugiego rzędu, prawdopodobieństwo przejścia do kolejnych węzłów zależy również od stanu poprzedniego.
Zamiast pojedynczych interakcji, będziemy analizować ich pary:
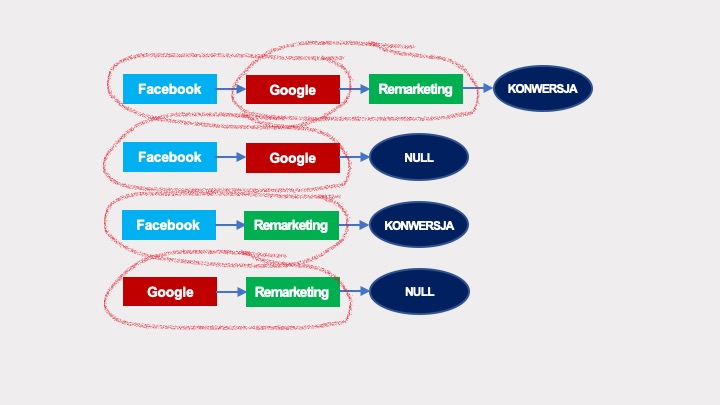
Graf łańcuchów Markowa będzie wyglądał w tym przypadku następująco:

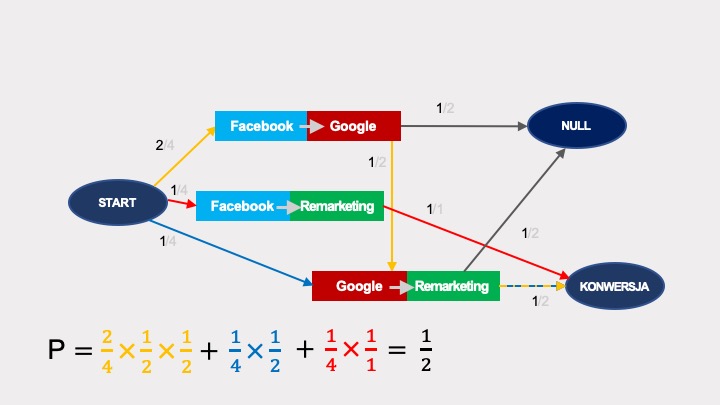
Obliczenia prawdopodobieństw wykonywane są w sposób analogiczny jak w przypadku łańcuchów Markowa pierwszego rzędu. Prawdopodobieństwo przejścia do konwersji (co jest możliwe na trzy sposoby, zaznaczone kolorami) wyliczane na podstawie tego grafu wynosi niezmiennie 1/2:
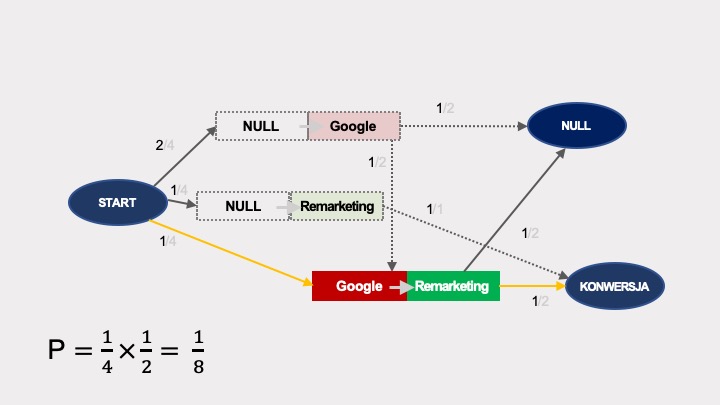
W podobny sposób obliczamy efekty usunięcia. Usunięcie Facebooka spowoduje zniknięcie wszystkich węzłów par interakcji zawierających Facebooka:
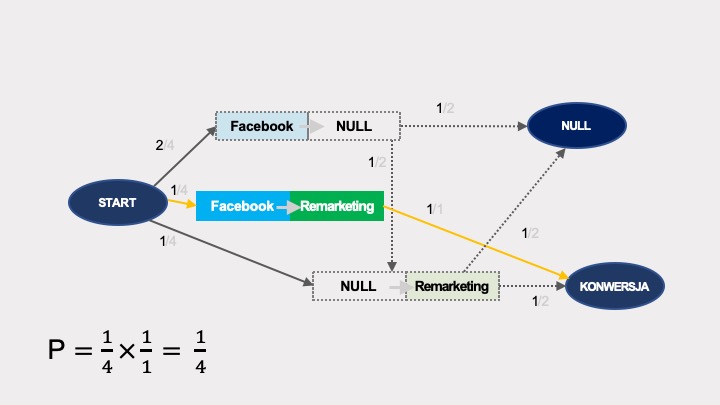
Analogicznie wyliczamy efekt usunięcia dla Google’a:
… oraz dla remarketingu:
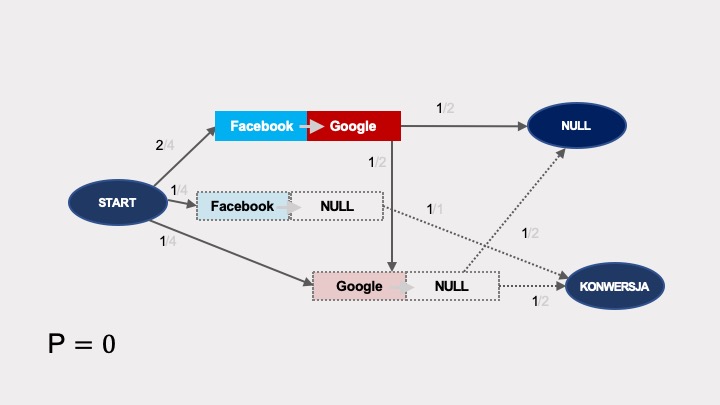
Obliczenia efektów usunięcia i udziałów w wyniku są identyczne, jak we wcześniejszych przykładach:
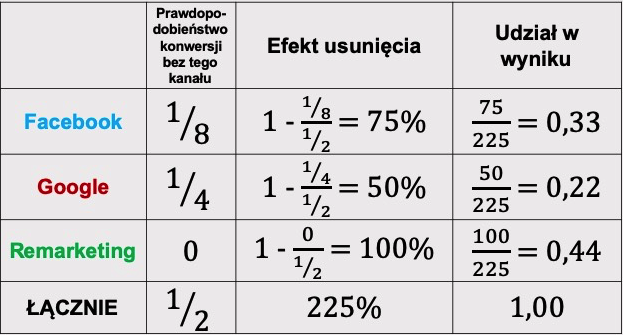
W ogólności, można tworzyć łańcuchy Markowa trzeciego, czwartego i dalszych rzędów. Ich węzły będą miały jeszcze dłuższą “pamięć” i prawdopodobieństwo przejścia do kolejnych węzłów będzie zależało od dwóch, trzech itd. poprzednich stanów.
Jeśli będziesz wykorzystywać łańcuchy Markowa wyższego rzędu, zauważysz, że atrybucja wyliczenia na podstawie łańcuchów kolejnych rzędów już niewiele różni się od siebie. W praktyce rzadko używa się łańcuchów wyższego rzędu niż 4.
Ścieżki jednokanałowe
Łańcuchy Markowa wykorzystują w obliczeniach znormalizowany efekt usunięcia. Jak już to było opisane w artykule dotyczącym wartości Shapleya, powoduje to pewien problem ze ścieżkami jednokałowymi, tj. takimi, na których występuje tylko jedna interakcja.
Zobaczmy poniższy przykład. Mamy na nim dwie ścieżki, z których jedna zawiera tylko jedną interakcję, Mail:
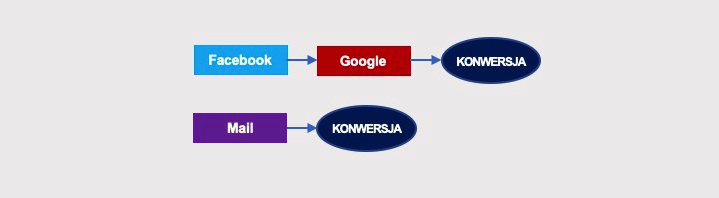
Graf łańcucha Markowa będzie wyglądał następująco (prawdopodobieństwa sumują się do jedności):
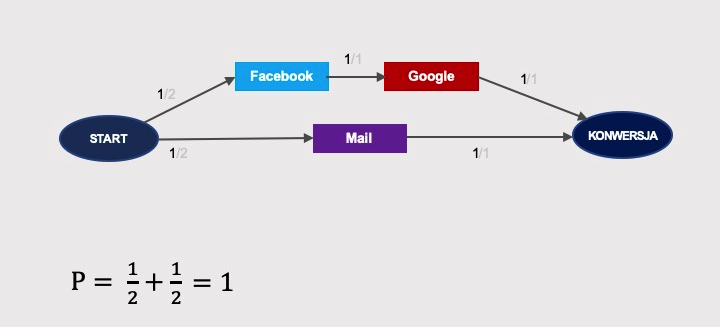
Obliczmy efekty usunięcia Facebooka:
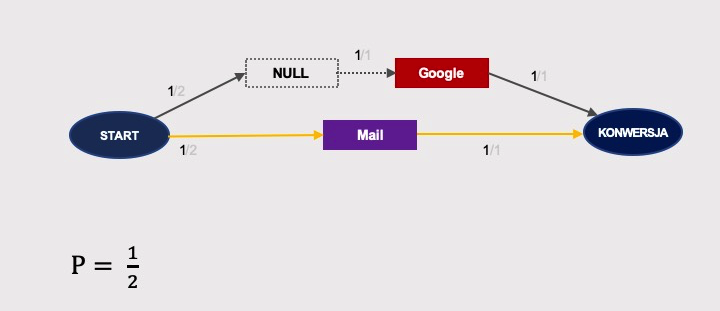
… Google’a …
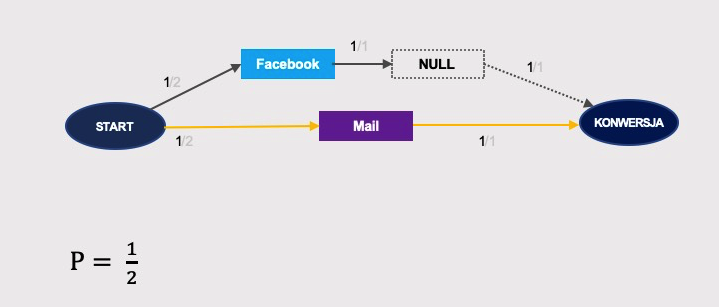
… oraz Maila:
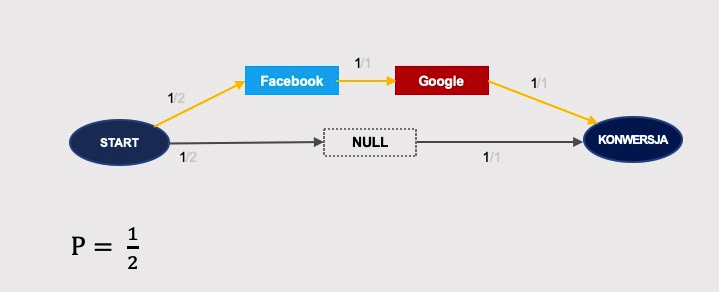
Obliczenia efektu usunięcia, udziału w wyniku i przypisanych konwersji wyglądają następująco:
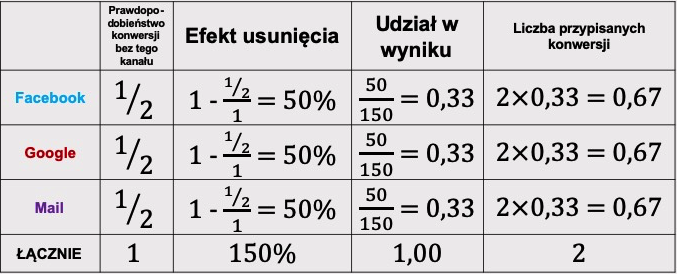
Zauważ, że w tym modelu atrybucji kanał Mail przyczynił się do 0,67 konwersji, co oznacza, że 0,33 konwersji zostało przypisana do Facebooka i Google’a. Skoro w konwersji, w której brał udział Mail, nie brała udziału żadna inna interakcja, to dlaczego innym kanałom przypisujemy część udziału w tej konwersji? To pozbawione logiki.
Świadczy to o tym, że atrybucja z wykorzystaniem łańcuchów Markowa już na poziomie teorii jest pewnym przybliżeniem.
Jednym ze stosowanych rozwiązań jest wyłączanie ścieżek jednokanałowych z analizy. Skoro w konwersji uczestniczy tylko jeden kanał, to atrybucja jest oczywista (przypisujemy ją temu właśnie jedynemu kanałowi) i nie ma potrzeby zaawansowanego modelowania.
Łańcuchy Markowa obliczamy tylko dla konwersji ze ścieżek, w których biorą udział dwa lub więcej kanałów, a następnie do tak obliczonej atrybucji doliczamy konwersje ze ścieżek jednokanałowych.
Właściwości łańcuchów Markowa
Atrybucja z wykorzystaniem łańcuchów Markowa jest alternatywą dla atrybucji na podstawie Wartości Shapleya.
Obarczona jest co prawda błędem wynikającym z wykorzystywania efektu usunięcia, który w wyniku normalizacji potrafi niesprawiedliwie odbierać wartość ścieżkom jednokanałowym i innym krótkim ścieżkom, ale ma wiele innych przydatnych cech.
Przede wszystkim, model ten jest znacznie mniej wrażliwy na przypadkowe dane o mniejszej istotności statystycznej, które potrafią kompletnie zniekształcić Wartość Shapleya. Dzięki temu, można go wykorzystywać w przypadku mniejszych zbiorów danych i przy większej granulacji kanałów.
Mimo pewnej złożoności związanej z pętlami grafu, jest mniej obciążający obliczeniowo od wartości Shapleya, dzięki czemu nadaje się do analizy większej liczby kanałów.
Łańcuchy Markowa dają wyniki oscylujące wokół wyników modelu liniowego. Nie wysyłają mocnych sygnałów w przypadku click spamu, jak to robi wartość Shapleya. Nie dostrzegają też braku wpływu interakcji typu conversion hijacking na łączny wynik (zob. też artykuł na temat Wartości Shapleya).
Niemniej, analiza atrybucji w modelu łańcuchów Markowa w porównaniu z modelem liniowym i innymi modelami, może dostarczyć wartościowych sygnałów do analizy.
Trzeba jednak pamiętać, że niezależnie od zastosowanej metody atrybucji, algorytmy takie, jak łańcuchy Markowa opierają się o analizę korelacji. Korelacja może wskazywać na istnienie związku przyczynowo-skutkowego między interakcją a konwersją, ale nie jest jego dowodem, dlatego nie wszystkie sygnały mogą być odczytywane bezbłędnie.
Ten artykuł dostępny jest też w wersji angielskiej.
Następny artykuł (cz. 12): Wspomaganie czy kanibalizacja
Warto przeczytać: Przewodnik po atrybucji w Google Analytics


