Założenie, że przychody z reklamy będą rosły proporcjonalnie do wydatków, okazuje się zazwyczaj nierealistyczne. Zależność między przychodem generowanym przez reklamę a jej kosztem jest najczęściej nieliniowa, a w miarę wzrostu wydatków możemy oczekiwać coraz mniejszych przyrostów krańcowych przychodu. Jak więc można tę funkcję opisać?
Dlaczego krańcowa efektywność spada?
Przynajmniej od pewnego momentu powinniśmy oczekiwać, że każde kolejne euro wydane na reklamę będzie przynosić coraz mniejszy zwrot.
Malejąca krańcowa efektywność reklamy wynika z wielu czynników. Jednym z powodów jest to, że zwiększanie inwestycji w dany kanał marketingowy wiąże się z koniecznością wyparcia większej liczby konkurentów.
Konkurencja w reklamie będzie najczęściej szersza niż nasza bezpośrednia konkurencja rynkowa. Będą to wszystkie firmy, które kierują się do tej samej grupy docelowej i pragną reklamować się w tych samych kanałach.
Oznacza to konieczność płacenia wyższych stawek za kliknięcie lub wyświetlenie reklamy, co szczególnie widoczne jest w systemach reklamowych, w których cena ustalana jest w aukcji w czasie rzeczywistym, takich jak Meta, Google i większość mediów społecznościowych czy sieci reklamowych RTB.
Remedium na to może być wejście w nowe kanały marketingowe, co też pozwoli na dotarcie do nowych odbiorców, ale w miarę wzrostu inwestycji będzie dochodziło do coraz większego pokrywania się grup odbiorców między kanałami (tzw. kanibalizacja).
Wreszcie, rosnąca częstotliwość wyświetleń i coraz większa liczba punktów styku konsumentów z reklamą powoduje ich mniejszą reakcję na kolejne ekspozycje reklamy.
Przykładowo, dwudzieste wyświetlenie reklamy prawdopodobnie wpłynie na odbiorcę w mniejszym stopniu, niż jej pierwsze wyświetlenie.
Czynników tych może być więcej. Wszystkie one są manifestacją uniwersalnej zasady ekonomii – prawa malejącej produktywności krańcowej. Mówi ono, każda dodatkowa jednostka nakładu na uzyskanie jakiegoś efektu przynosi coraz mniejszy jego przyrost.
Tworząc modele biznesowe oczekiwalibyśmy, by zależność między wydatkami na reklamę a przychodami dawała się ująć funkcją matematyczną, a nie tylko stwierdzeniem, że krańcowa korzyść będzie spadać.
Reklama w wyszukiwarce
W wyszukiwarce mamy do czynienia z ograniczoną liczbą dostępnych wyświetleń. Wolumen zapytań związany z określonym wyszukiwanym hasłem wynika z zachowania konsumentów i nie jesteśmy w stanie go zwiększyć podnosząc stawki CPC i wydając więcej na SEM.
Jeśli w danym okresie mamy przeciętnie 500 wyszukiwań słowa „wiertarka udarowa” dziennie, nie wpłyniemy na to inwestując więcej w reklamę na to słowo. Dla każdego z wyświetleń mamy ograniczoną liczbę miejsc reklamowych, może to być np. cztery płatne wyniki wyszukiwania na górze strony i osiem widocznych reklam produktowych – i to w zasadzie wszystko, co generuje jakiś istotny ruch. Nie bez powodu żartowało się, że więcej widziało ciemną stronę Księżyca niż drugą stronę w Google.
Jest więc oczywiste, że w pewnym momencie w SEM osiągniemy „sufit”. Podobne mechanizmy bedą występować rzecz jasna również w innych mediach reklamowych.
W przypadku SEM w znacznie mniejszym stopniu będziemy mieli do czynienia ze zmniejszoną odpowiedzią użytkownika na kolejne kontakty z reklamą, gdyż są one inicjowane przez użytkownika, który z jakiegoś powodu wciąż szuka w wyszukiwarce, a nie kieruje się na naszą stronę.
Kampanie w wyszukiwarce będą też w mniejszym stopniu dawały efekty odłożone w czasie. SEM to działania „direct response” i pomijając typowy dla danego produktu upływ czasu między interakcją a konwersją (dłuższy lub krótszy proces decyzyjny), mają one ograniczony wpływ np. na długofalową świadomość marki.
Dlatego na relację między kosztem a przychodem z reklamy w wyszukiwarce będą mieć wpływ przede wszystkim mechanizmy związane z konkurencją między reklamodawcami w samej wyszukiwarce.
Na koszt reklamy będzie wpływać też polityka cenowa wyszukiwarek. Koszty kliknięcia ustalane są co prawda w aukcji, ale Google i inne wyszukiwarki stosują dodatkowe mechanizmy, które pozwalają im oddziaływać na CPC.
Przykładowo, stawka minimalna za wyświetlenie reklamy i za wyświetlenie na górze strony nie pozwoli nam kupić reklamy za bezcen, nawet jeśli na dane słowo nie ma żadnej konkurencji lub chwilowo innym reklamodawcom skończył się budżet.
Należy zakładać, że algorytmy aukcji Google i innych wyszukiwarek zmierzają do ustalania CPC na poziomie, przy którym ich przychody będą największe, biorąc pod uwagę aktualny popyt i gotowość reklamodawców do akceptacji danej ceny.
Typowa zależność przychodu i kosztu w wyszukiwarce
Na podstawie danych z planera skuteczności Google Ads można określić, ile przychodu (konwersji) uda się uzyskać z kampanii w miarę zwiększania budżetu. Przykładowy rozkład wartości wygląda tak, jak poniżej:
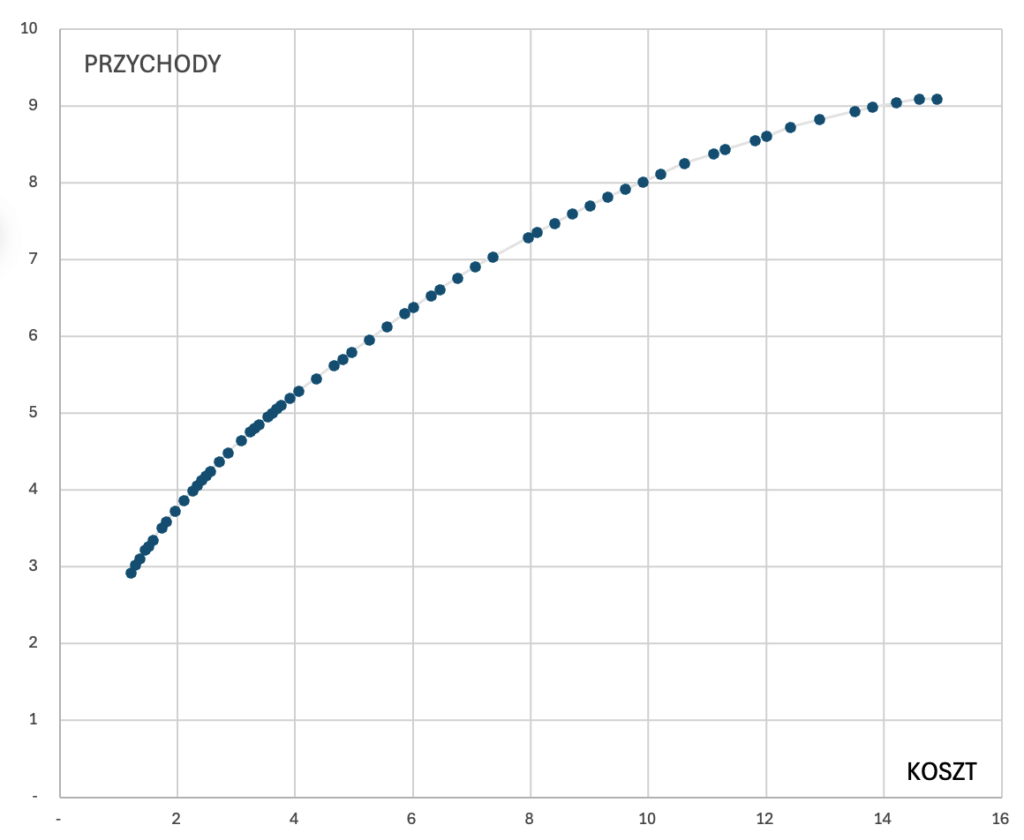
Jaką funkcją matematyczną można opisać tę relację? Funkcja ta będzie powinna:
- być funkcją rosnącą (wyższe wydatki oznaczają wyższe przychody);
- być funkcją wklęsłą (rosnąć coraz wolniej, przez co jej wykres będzie się zakrzywiać);
- mieć asymptotę poziomą, czyli pewną maksymalna wartość, której nigdy nie przekroczy (każdy kanał marketingowy ma swój „sufit”);
- dla kosztu = 0 mieć również wartość zero.
Aby zidentyfikować matematyczną relację między przychodem (R, Revenue) i kosztem (C, Cost), warto się przyjrzeć relacjom między pokrewnymi parametrami i poszukać tam zależności (najlepiej) liniowych.
Liniowo rosnący ERS w funkcji przychodów (stała elastyczność)
Najczęściej stosowaną miarą rentowności jest ROAS (Return On Ad Spend), jednak w analizie kosztów krańcowych dogodniejszą miarą będzie ERS (Effective Revenue Share), który jest matematyczną odwrotnością ROAS:
ERS = C/R = 1/ROAS
W odróżnieniu od ROAS, współczynnik ERS, podobnie jak CPC i CPA, rośnie w miarę intensyfikacji kampanii i z tego powodu jest bardziej intuicyjną miarą jednostkowego kosztu uzyskania przychodu.
Zależność ERS od przychodu kampanii w tym przykładzie wygląda następująco:
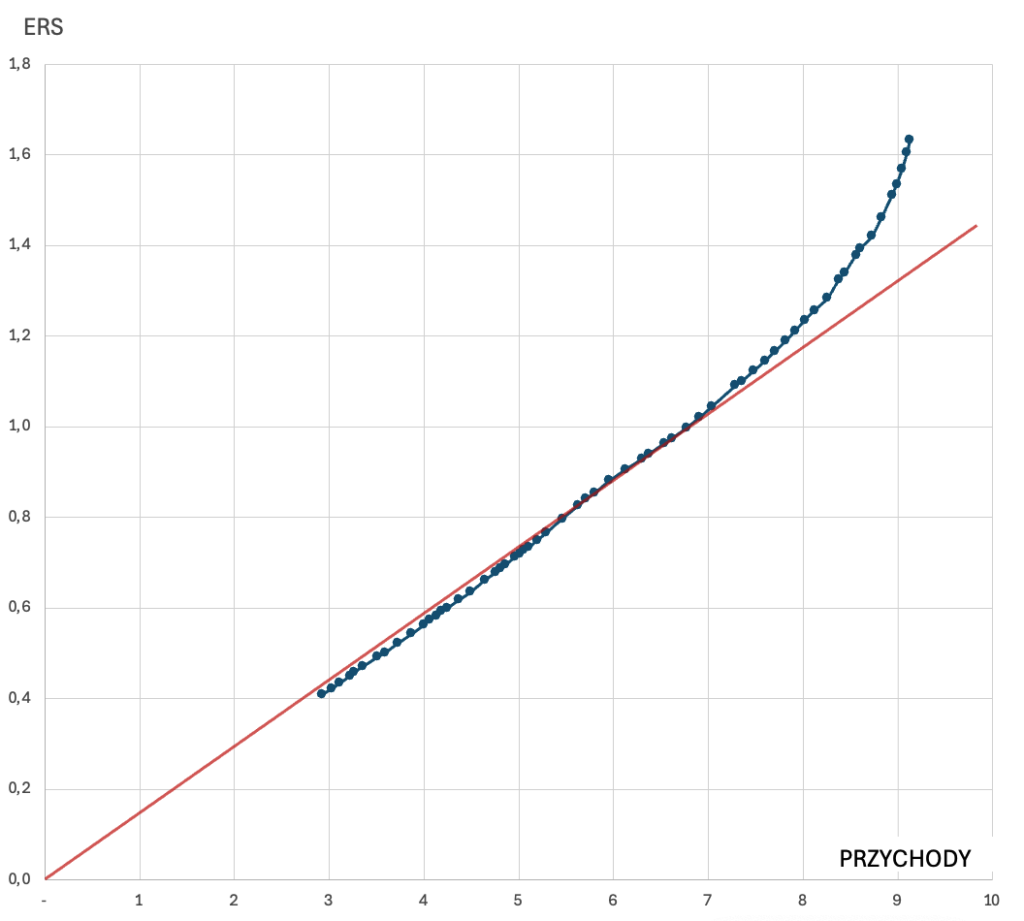
Jak widać, w dość znacznym przedziale jest to funkcja liniowa, która dopiero przy przychodach powyżej 7 (mln zł) zaczyna się zakrzywiać.
Liniowa zależność między ERS a przychodem oznacza, że elastyczność cenowa podaży konwertującego ruchu w tym przypadku jest stała. Elastyczność cenową definiujemy następująco:
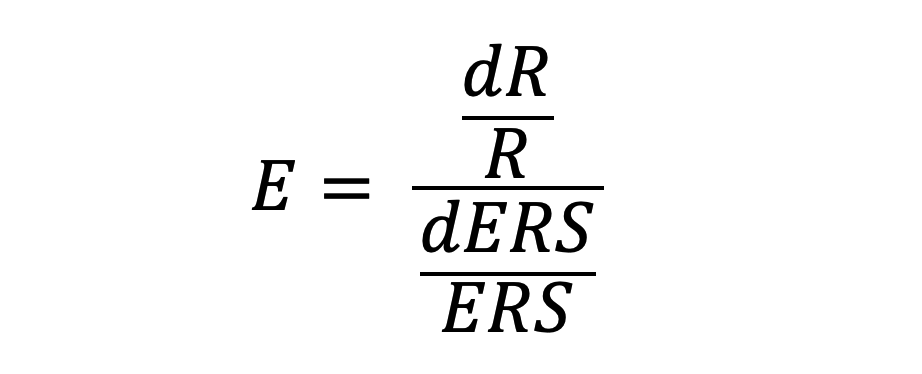
gdzie d oznacza bardzo mały przyrost.
Jest to więc stosunek względnego (procentowego) przyrostu przychodu do względnego przyrostu ceny. Elastyczność mówi nam, jak szybko rosną generowane przychody w miarę podnoszenia stawek i zwiększania akceptowanego kosztu ich uzyskania. W naszym przypadku oscyluje ona wokół wartości E = 0,94.
Elastyczność bliska jedności bardzo często spotykana jest w aukcjach reklamowych, gdyż jest to wartość maksymalizująca zyski wyszukiwarki. Przyczyny tego zjawiska opisuje szczegółowo ten artykuł w Magazynie Online Marketing.
Zakładając, że elastyczność jest stała, funkcja opisująca zależność przychodu od kosztu ma postać:
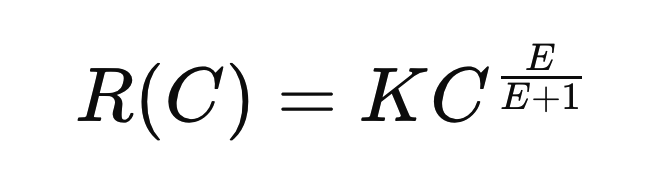
gdzie K jest stałą, którą możemy wyznaczyć z aktualnych wartości. Wyprowadzenie tego wzoru znajdziesz tutaj (plik PDF).
Oto, jak wygląda ta funkcja zastosowana do omawianej symulacji:
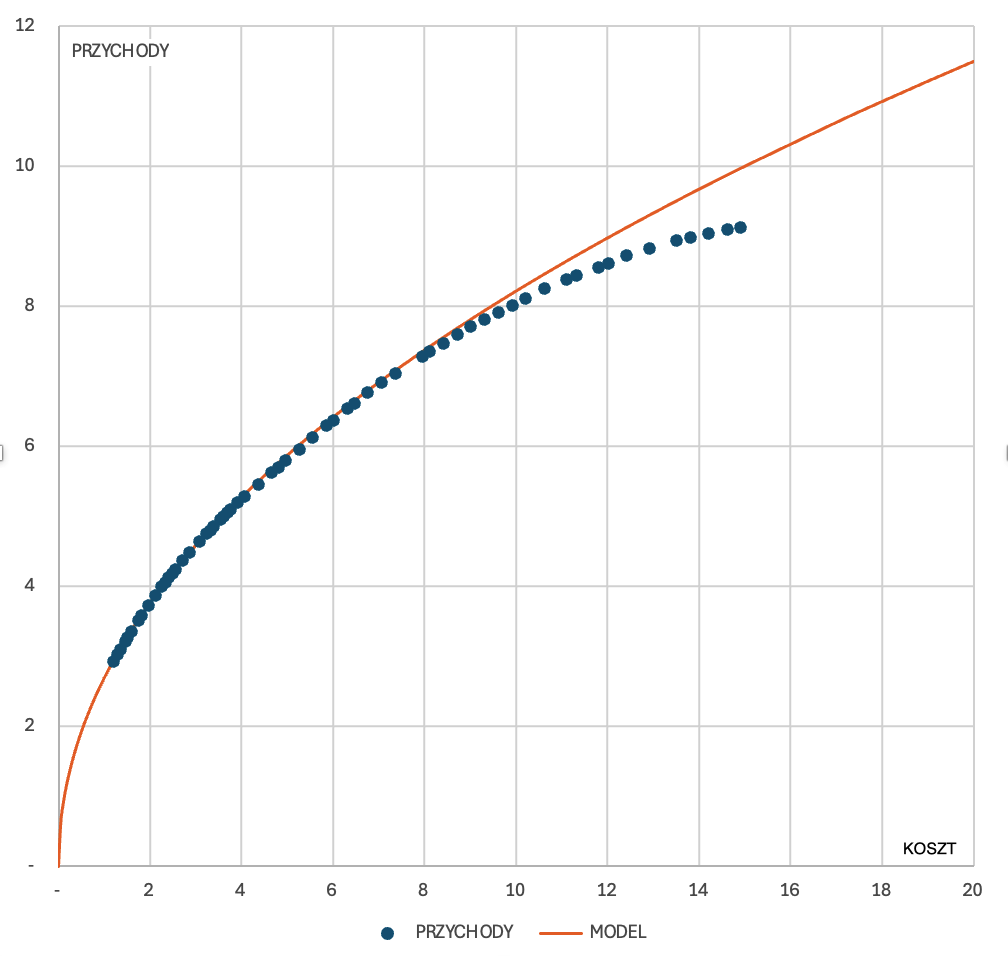
Jak widać, bardzo dobre odwzorowuje ona wartości z symulacji w szerokim zakresie. Rozbieżności zaczynają się pojawiać po przekroczeniu 8 (mln zł) kosztu.
Funkcja ta jednak nie ma asymptoty poziomej: dla nieskończonego kosztu jej wartość będzie zmierzała do nieskończoności, dlatego jej stosowanie zawsze będzie ograniczone do pewnego zakresu wydatków.
Jest to również dowód na to, że elastyczność cenowa nie może być stała i musi spadać w miarę wzrostu wydatków, co oznacza, że spadek efektywności musi być coraz szybszy.
Liniowo rosnący ERS w funkcji wydatków
Zależność ERS od kosztu kampanii w tym przykładzie wygląda następująco:
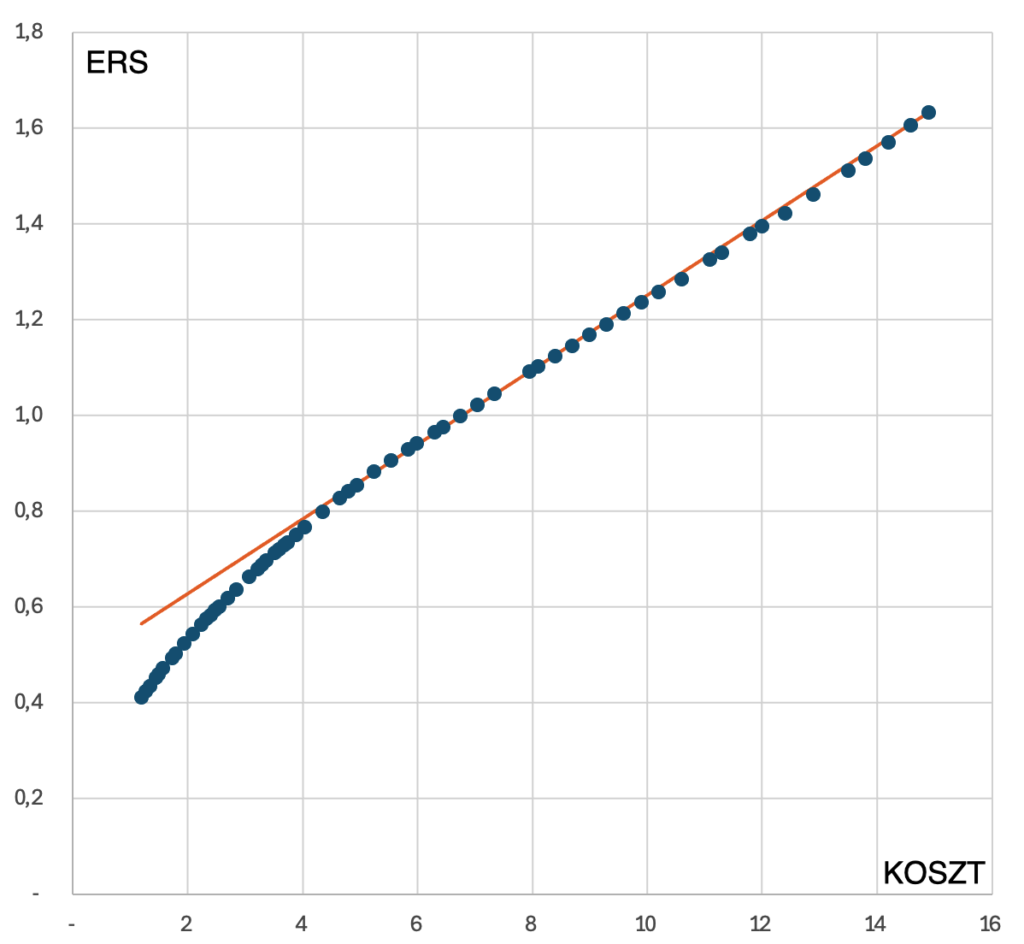
Rozkład wartości jest bliski liniowemu dla kosztów powyże 8 (mln zł). Jeśli zależność tę opiszemy:
ERS = aC + b
czyil
C/R = aC + b
to funkcja opisująca zależność przychodu od kosztu będzie miała postać:
R(C) = C / (aC + b)
Funkcja ta (linia zielona) będzie pokrywała się z wartościami symulacji dla kosztów powyżej 8 (mln zł):
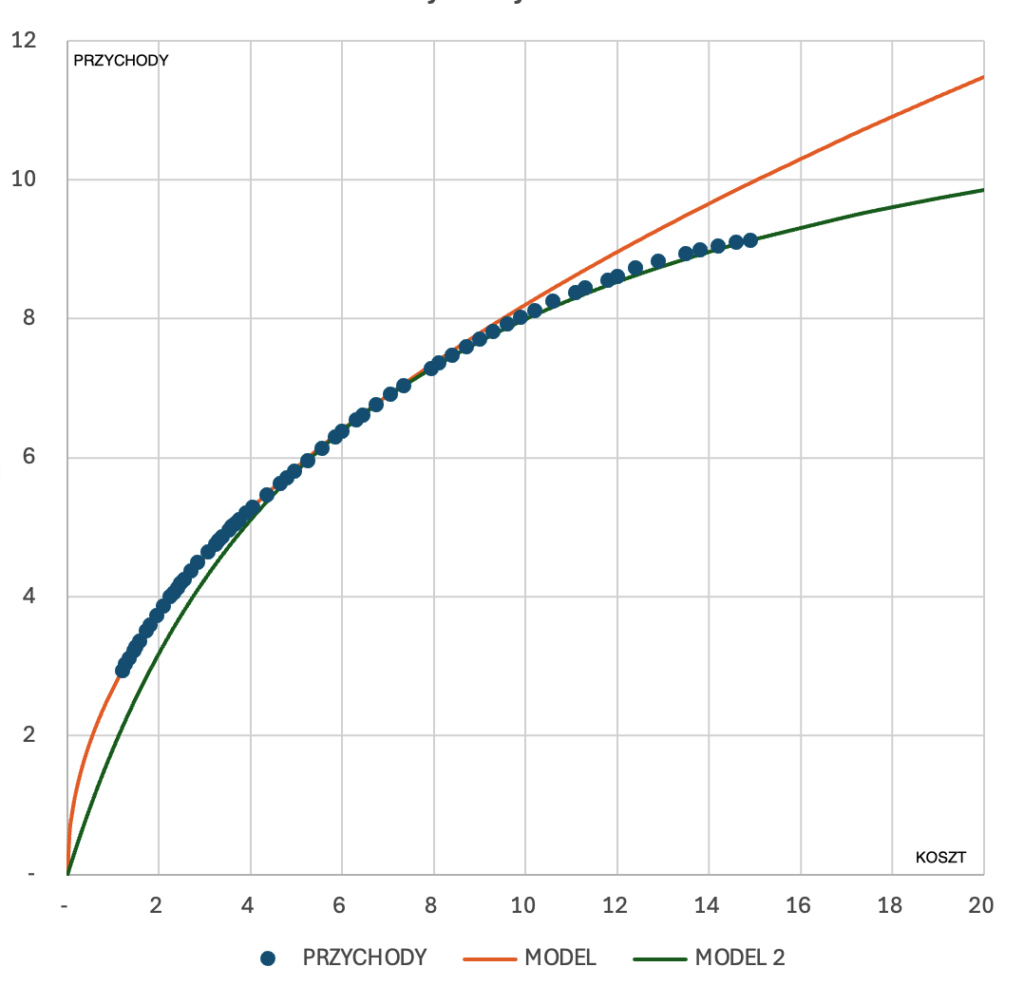
Funkcja ta (linia zielona) ma asymptotę poziomą: jej wartość w nieskończoności zmierza do 1/a (w tym przypadku jest to wartość 12,8 – tyle wg tej symulacji wynosi maksymalny przychód z tej kampanii, nawet gdybyśmy zainwestowali w nią nieograniczoną sumę pieniędzy).
Można więc zapisać Rmax = 1/a. Obliczmy teraz koszt C½ potrzebny do wygenerowania połowy maksymalnego przychodu, Rmax / 2 = 1/(2a), podstawiając te wartości do wzoru na R(C) i rozwiązując równanie:
1/(2a) = C½ / (aC½ + b)
czyli
C½ = b/a
Dlatego funkcję R(C) = C / (aC + b) możemy też zapisać w postaci:
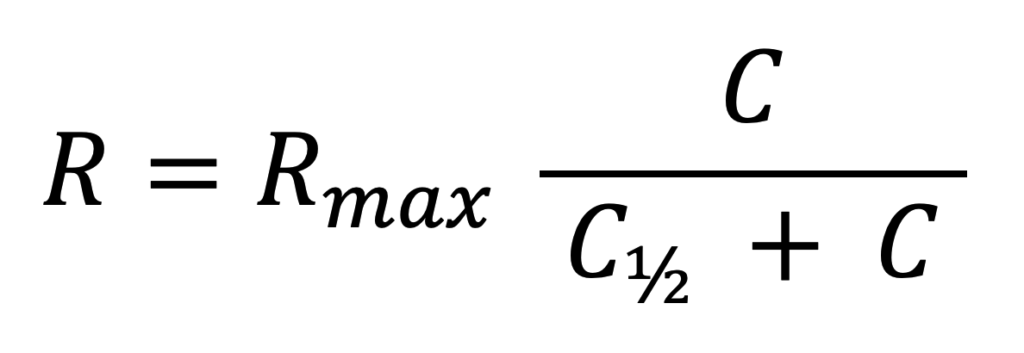
W z modelem na bazie stałej elastyczności (linia pomarańczowa), funkcje te pozwalają modelować kampanię w szerokim zakresie przychodów i kosztów.
Funkcja Hilla
W modelowaniu przychodów z reklamy można też wykorzystać funkcję Hilla. Funkcja ta wywodzi się z biochemii jest stosowana przede wszystkim do opisu procesów fizjologicznych, np. procesu wiązania tlenu z hemoglobiną we krwi lub do przewidywania, jak różne stężenia toksyn wpływają na organizmy.
Okazuje się, że dobrze nadaje się do modelowania efektywności reklamy. Jej postać jest następująca:
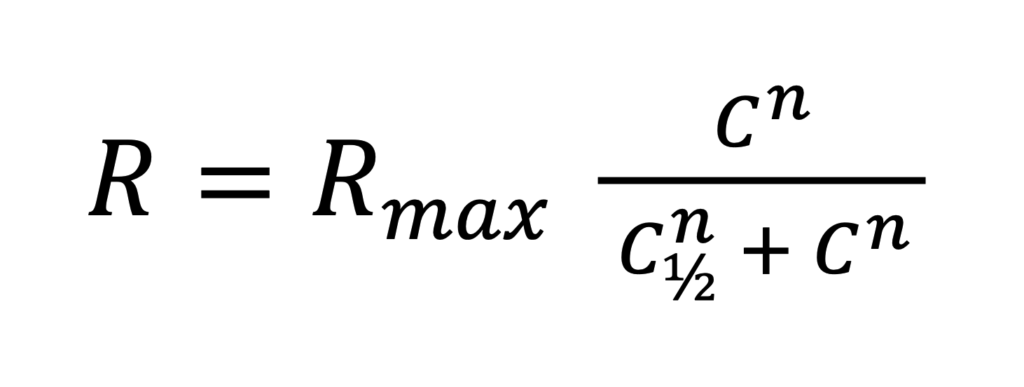
Rmax – maksymalna wartość przychodu możliwego do wygenerowania z danej reklamy („sufit”)
C½ – koszt osiągnięcia połowy maksymalnego możliwego przychodu, tj. wartość kosztu C, dla którego funkcja R(C) ma wartość:
R(C½) = 1/2 Rmax
n – współczynnik determinujący kształt funkcji:
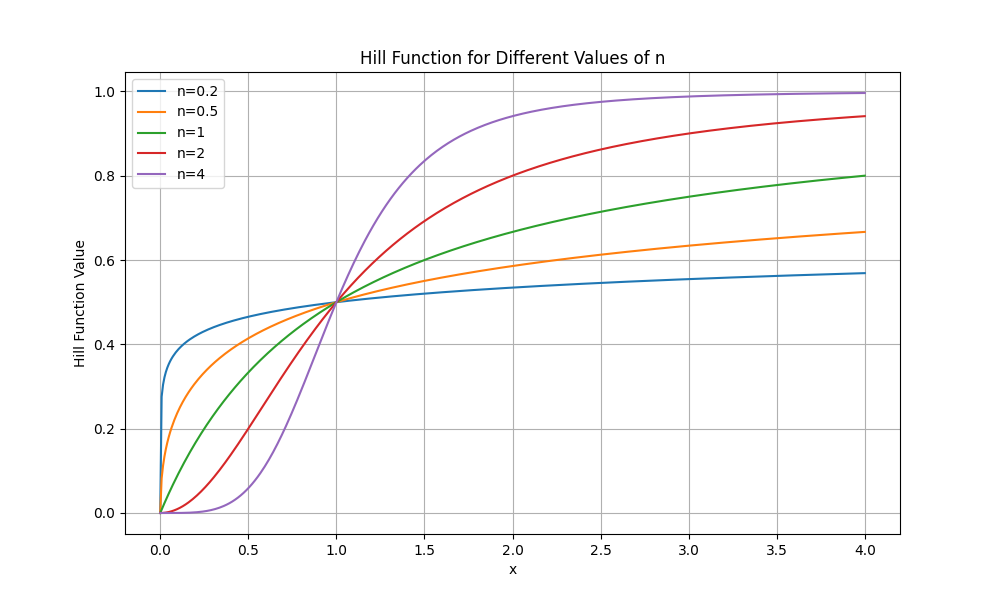
Funkcja ta spełnia więc zakładane warunki: jest rosnąca, przechodzi przez punkt (0, 0), ma asymptotę poziomą (Rmax), a dla wartości n ≤ 1 jest funkcją wklęsłą. Dla n = 1 uzyskujemy model tożsamy z modelem liniowej funkcji ERS(C) opisanej wcześniej.
Do omawianego przykładu najlepsze dopasowanie funkcji Hilla otrzymujemy dla Rmax = 23.36, C½ = 29.02, n = 0.62.
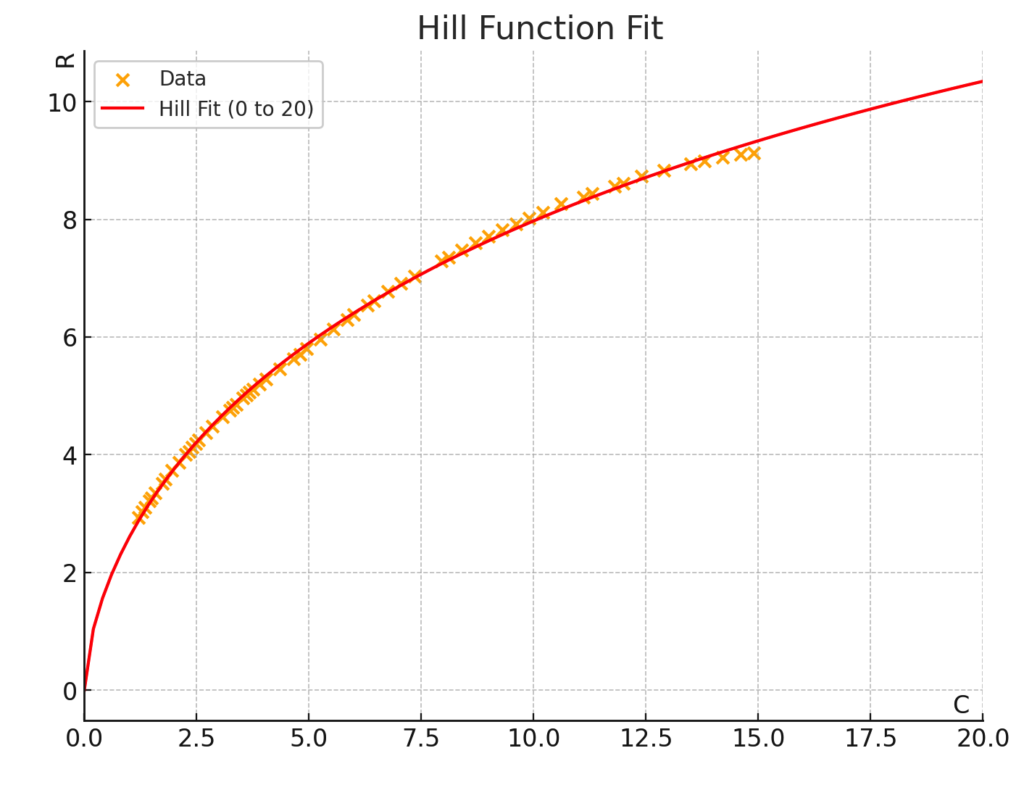
Funkcja Hilla nie jest jednak uniwersalnym rozwiązaniem dokładnego odwzorowania każdej funkcji R(C). Często będzie trzeba korzystać ze złożenia dwóch lub więcej funkcji dla różnych przedziałów wydatków (zob. inne przykłady rozkładów R(C) w tym pliku PDF).
Oczywiście pozostaje pytanie, czy kilkuprocentowe odchylenie od modelu jest realnym problemem dla prognozowania o tak wysokiej niepewności, jak prognozowanie wyników reklamy.
Może Cię również zainteresować artykuł na temat modelowania optymalnego poziomu wydatków w kampanich e-commerce.


