W analizie atrybucji wykorzystywane są modele matematyczne, które stanowią podstawę modelowania algorytmicznego. Jedną z koncepcji, która znalazła tu zastosowanie, jest Wartość Shapleya. W jaki sposób może ona nam pomóc w modelowaniu atrybucji?
Poprzedni artykuł (cz. 9): Model oparty na danych (Data-driven)
We wcześniejszych artykułach z tego cyklu przedstawione zostały różne modele atrybucji, od najprostszych modeli single-touch po złożone modele multi-touch.
Jednak nawet najbardziej rozbudowany, niestandardowy model atrybucji będzie wymagał arbitralnego określenia modelu bazowego, a także wag, jakie przyznajemy w tym modelu poszczególnym interakcjom (wyświetleniom reklamy, kliknięciom, obejrzeniom filmu).
Niestety, odpowiedzi na pytanie, jak to zrobić, jest jak na lekarstwo. Najczęściej możemy się spotkać z radą by “testować różne modele, by określić, który najbardziej sprawdzi się w Twoim przypadku” lub “musisz się zastanowić, co jest dla Ciebie najważniejsze i dostosować…”.
Temu problemowi, wspólnemu dla wszystkich, jak się to określa, heurystycznych modeli atrybucji, mają zaradzić modele algorytmiczne, które na podstawie dostępnych danych o ścieżkach konwersji wyciągają wnioski co do znaczenia poszczególnych interakcji dla wygenerowania konwersji.
Jedną z koncepcji stosowanych w algorytmicznych modelach atrybucji jest Wartość Shapleya.
Czym jest Wartość Shapleya?
Wartość Shapleya jest pojęciem z teorii gier. Określa, jakiego wynagrodzenia powinien się spodziewać gracz w grze zespołowej, biorąc pod uwagę jego średni wkład do wyniku tej gry uzyskanego przez każdą z możliwych kombinacji graczy.
Do zrozumienia Wartości Shapleya, konieczne jest zaznajomienie się z pojęciem wkładu marginalnego. W grach zespołowych, każdy z graczy ma pewien wkład w łączny wynik. Jeśli w grze możliwe są różne kombinacje graczy, którzy do niej wchodzą (różne koalicje), to korzyść z przyjęcia do niej danego gracza (wzrost wyniku gry) może być różna dla każdej z tych kombinacji.
Wkład marginalny gracza i do danej kombinacji graczy obliczamy w sposób następujący:

Innymi słowy, wkład marginalny określa, ile określona kombinacja graczy zyska na wyniku, jeśli dołączy do niej dany gracz.
Możliwych kombinacji graczy może być wiele. Mogą one mieć różny rozmiar (liczebność). Najprostsza kombinacja to taka, w której bierze udział tylko dany gracz (rozmiar 1). Następnie może on utworzyć “dwuosobowe” kombinacje z każdym z innych graczy (rozmiar 2). I tak dalej, aż do kombinacji, w której biorą udział wszyscy gracze (rozmiar n, gdzie n to łączna liczba graczy). Czyli, kombinacje będą występować w n różnych rozmiarach, od 1 do n.
Wartość Shapleya oblicza się w następujący sposób: Dla wszystkich kombinacji graczy zawierających danego gracza, sumujemy wkłady marginalne tego gracza, podzielone przez liczbę kombinacji danego rozmiaru – a następnie dzielimy przez liczbę graczy:

Podział dochodu między przedsiębiorcę i pracowników
Spróbujmy teraz wyjaśnić Wartość Shapleya na przykładzie. Wyobraźmy sobie przedsiębiorstwo, w skład którego mogą wchodzić biznesmen B oraz pracownicy: P1, P2, P3. Każdy z pracowników jest w stanie wytworzyć przychód w wysokości 1 sakiewki. Firma, w której biznesmen zatrudnia 3 osoby, zarabia 3 sakiewki:
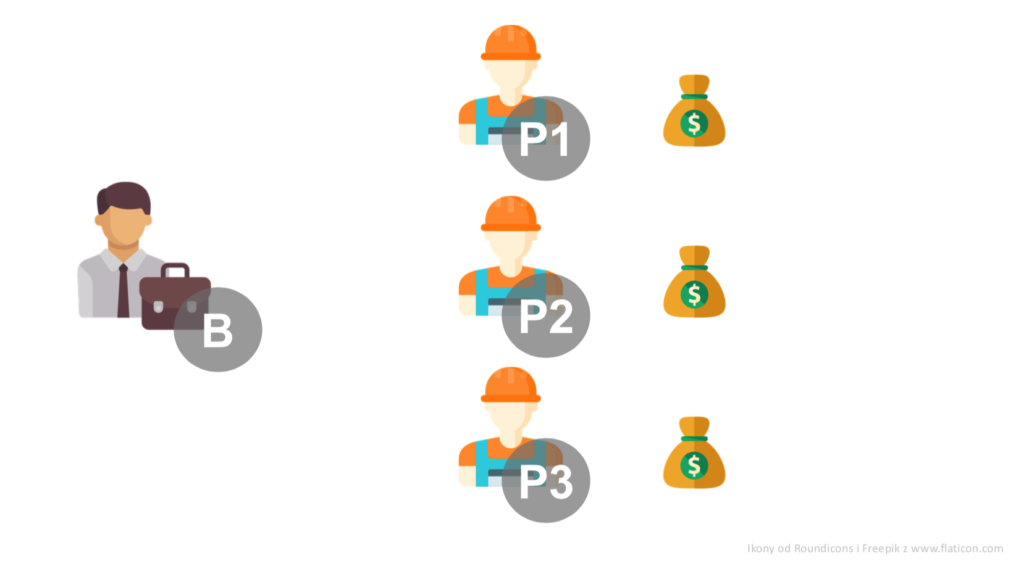
Jeśli pracowników będzie dwóch, firma zarobi tylko 2 sakiewki. Nie ma tu znaczenia, czy będą pracowali P1 z P2, czy P2 z P3, czy też P1 z P3 – dowolnych dwóch pracowników zatrudnionych przez biznesmena zawsze zarobi 2 sakiewki. Jeśli pracownik będzie tylko jeden, zarobi tylko jedną sakiewkę. Sam biznesmen bez pracowników nie zarobi nic. Bez biznesmena, sami pracownicy nie będą w stanie nic zarobić, niezależnie od tego, ilu ich będzie.
Zobaczmy teraz, jak liczyć wkłady marginalne – na przykładzie gracza P3. Do kombinacji B, P1, P2 (biznesmena zatrudniającego dwóch pozostałych pracowników) gracz P3 wniesie 1 sakiewkę, bo tyle wynosi różnica między dochodem firmy z pracownikiem P3 (tj. w składzie B, P1, P2, P3) i bez niego (w składzie B, P1, P2):

Z kolei do kombinacji P1, P2 (czyli dwóch pracowników, ale bez biznesmena), gracz P3 marginalnie nie wnosi nic. Z nim, czy bez niego – zarobek jest zerowy:
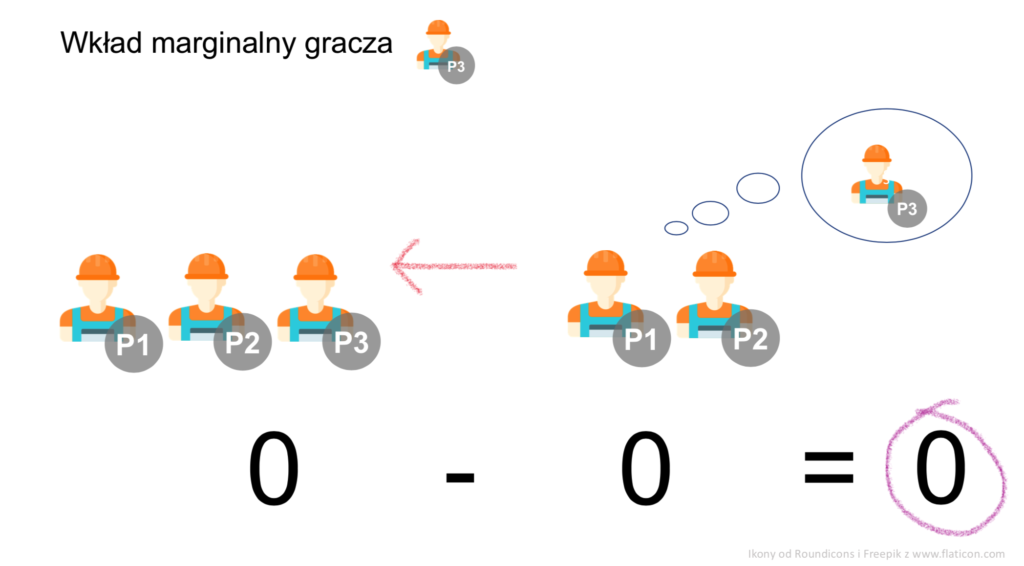
W naszej grze mamy łącznie czterech graczy (P1, P2, P3, B). Mogą oni się łączyć w 1, 2, 3 i 4-osobowe kombinacje. Kombinacje z udziałem danego gracza, np. gracza P1, to:
- jedna kombinacja jednoosobowa (on sam),
- trzy kombinacje 2-osobowe,
- trzy kombinacje 3-osobowe,
- jedna kombinacja 4-osobowa (wszyscy gracze):
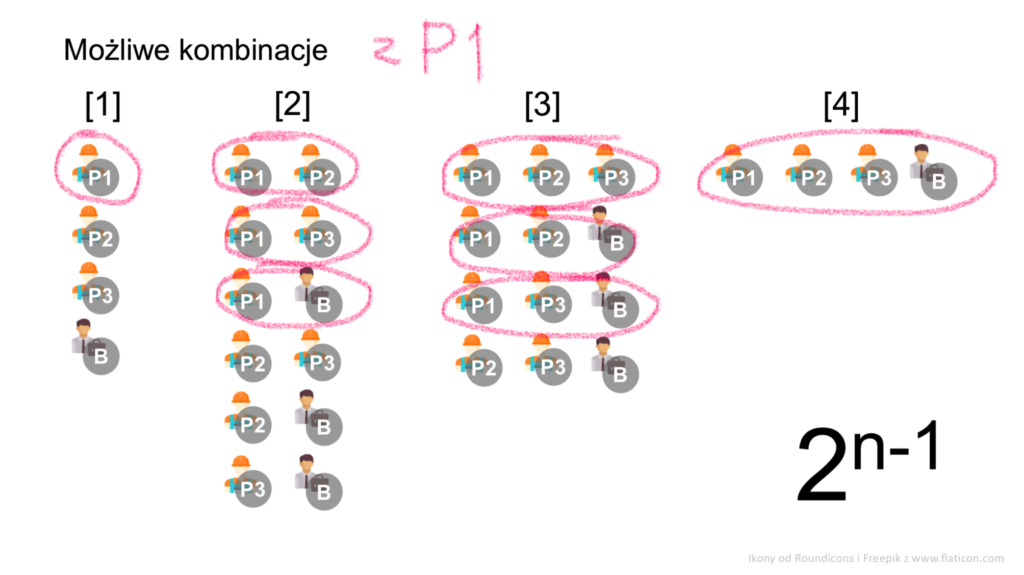
Łącznie tych kombinacji jest 8. W ogólności, kombinacji, w których wziąć udział dany gracz, jest 2n-1, gdzie n to liczba graczy (w tym przypadku jest to 2(4-1) = 23 = 8).
Zobaczmy teraz, jak będą wyglądać wkłady marginalne gracza P1 do każdej z możliwych kombinacji z jego udziałem, a następnie dokonajmy obliczeń zgodnie z definicją Wartości Shapleya:
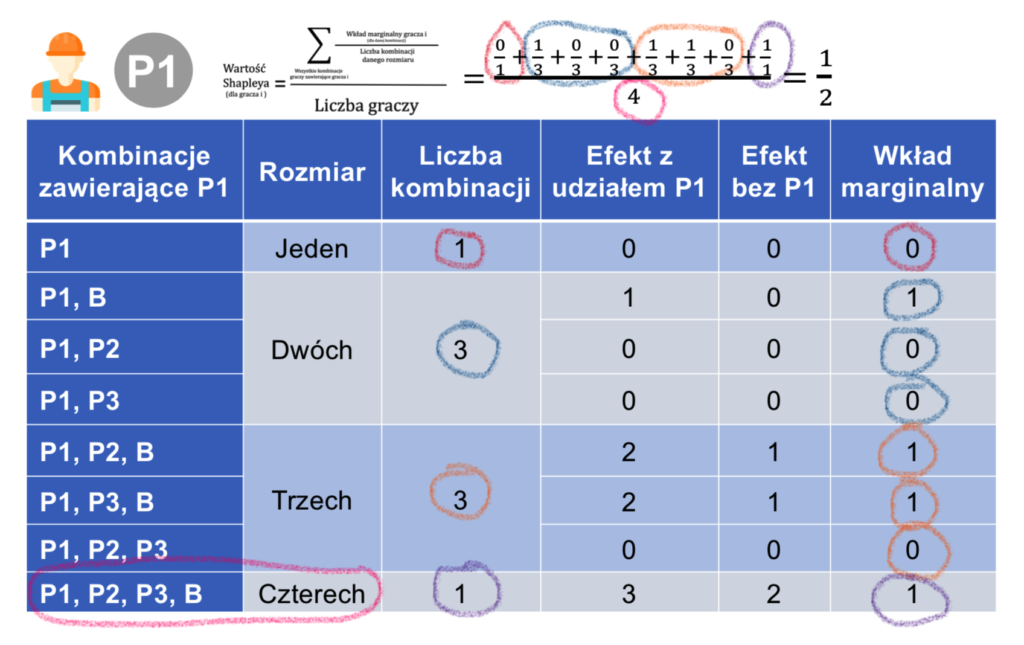
Obliczyliśmy, że wartość Shapleya dla gracza P1 wynosi Sh(P1) = 1/2 = 0,5. Podobne obliczenia należałoby wykonać dla pozostałych graczy, ale możemy też wykorzystać właściwości Wartości Shapleya i dokonać obliczeń na skróty.
Ponieważ rola graczy P1, P2 i P3 jest identyczna, Wartość Shapleya dla tych graczy również będzie taka sama, czyli Sh(P2) = 0,5 oraz Sh(P3) = 0,5.
Firma w pełnej obsadzie (P1, P2, P3, B) wytwarza 3 sakiewki. Biznesmen powinen otrzymać to, co zostanie z łącznego wyniku po “wypłaceniu” Wartości Shapleya pracownikom:
Sh(B) = 3 – Sh(P1) – Sh(P2) – Sh(P3) = 3 – 0,5 – 0,5 – 0,5 = 1,5
W ogólności, w grze biznesmen – pracownicy, Wartość Shapleya dzieli wypracowany zysk w ten sposób, że połowa zysku przypada na biznesmena, drugą połowę dzielą między sobą pracownicy po równo.
Wartość Shapleya dla ścieżek konwersji
Zobaczmy teraz, jak obliczyć Wartość Shapleya dla gry, w której różne kanały marketingu wypracowują wspólny wynik.
Na początku trzeba określić, co będzie wynikiem w naszej grze – czyli, jakby powiedział matematyk, co będzie funkcją charakterystyczną. Pierwsze, co przychodzi na myśl w tym przypadku, to wynik w postaci liczby konwersji. W Google Analytics znajdziemy dane na temat konwersji generowanych przez poszczególne ścieżki:
W naszym przykładzie założymy, że mamy trzy źródła: Facebook, Google i Affiliate.
Zauważ, że w modelu Shapleya nie ma znaczenia kolejność wystąpienia kanałów na ścieżkach. Przykładowo, ścieżki:
- Facebook > Google
- Google > Facebook
- Google > Facebook > Google > Google > Facebook
- Google > Facebook > Google
– sumujemy do jednej kombinacji kanałów Facebook + Google.
Oto liczba konwersji wygenerowana przez poszczególne kombinacje kanałów:
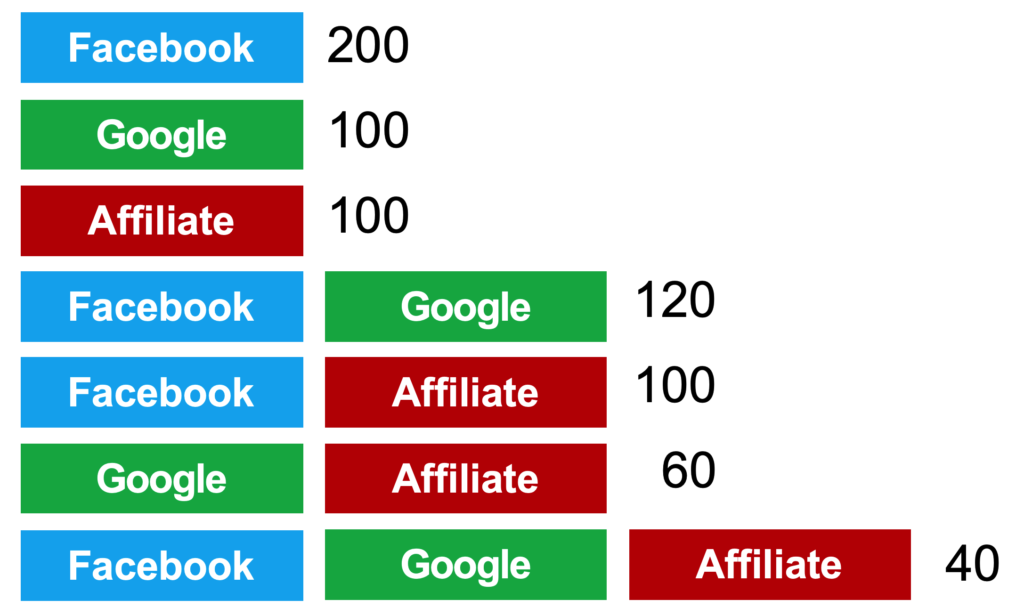
Zauważ też, że gdy wykorzystujemy Facebooka i Google, to będziemy uzyskiwać konwersje na ścieżkach zawierających zarówno kombinację Facebook + Google, jak i działające w pojedynkę Google i Facebooka. Jeśli w grze będą brały udział wszystkie trzy kanały, to nasz wynik będzie zawierał konwersje generowane przez wszystkie kombinacje kanałów.
Innymi słowy, aby uzyskać liczbę konwersji dla danej kombinacji, musimy skumulować wartości ścieżek, które się w tej kombinacji zawierają:

Gdybyśmy przyjęli, że wynikiem jest po prostu liczba konwersji dla danej kombinacji, uzyskiwalibyśmy bardzo często ujemne wartości wkładów marginalnych. Jeśli dwa kanały rzadko by się na siebie nakładały, ich połączenie generowałoby bardzo mało konwersji, co byłoby odczytane jako ujemy wkład marginalny – widać więc, że to nie miałoby sensu.
Obliczmy teraz Wartość Shapleya dla kanału FB. Zestawmy liczbę konwersji dla wszystkich kombinacji, w których FB bierze udział, z konwersjami tych kombinacji pozbawionych FB. Następnie obliczmy wkłady marginalne i podstawmy do formuły na Wartość Shapleya:
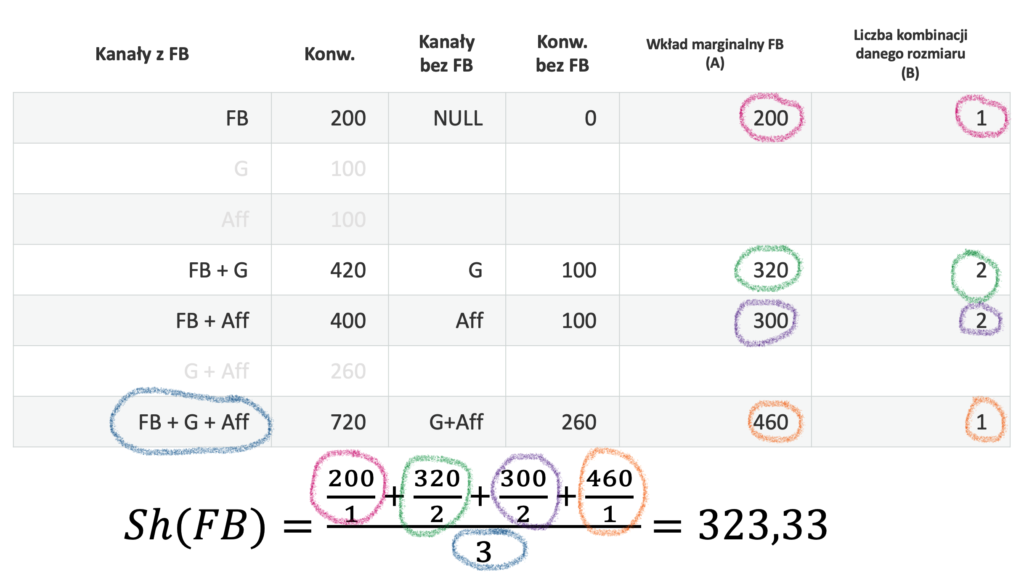
Uzyskaliśmy Sh(FB) = 323,33. Moglibyśmy teraz obliczać dalsze obliczenia, ale… tak naprawdę tracimy czas. Okazuje się, że przy tak rozumianym wyniku gry (przy takiej funkcji charakterystycznej), Wartość Shapleya upraszcza się do następującej formuły:
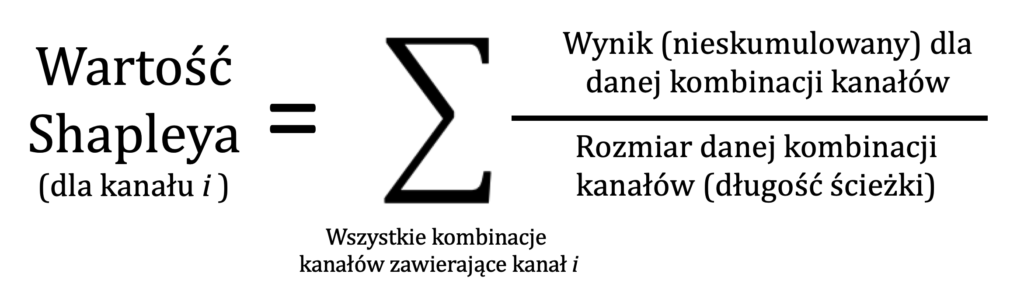
Oznacza ona, że Wartość Shapleya można obliczyć w następujący sposób: dla każdej ścieżki dzielimy wartość wygenerowanych konwersji przez długość tej ścieżki (liczbę interakcji na ścieżce), a następnie sumujemy tak uzyskane wartości dla wszystkich ścieżek. Dowód matematyczny tego twierdzenia można znaleźć tutaj (PDF w j. ang, Appendix, str. 19-20).
W ten sposób możemy obliczyć Wartość Shapleya znacznie prościej:
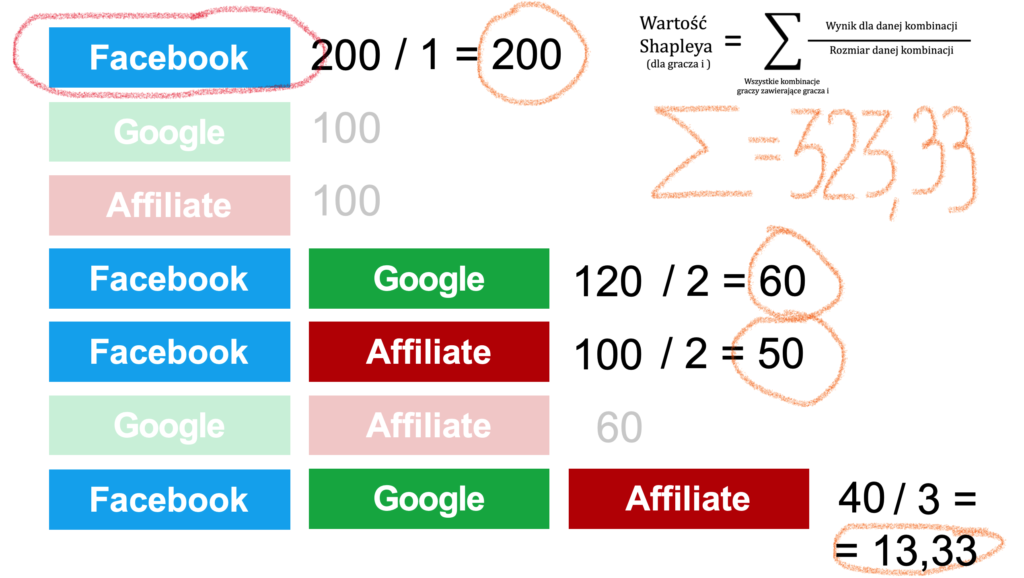
Wygląda znajomo? Tak, wartość Shapleya liczona na podstawie danych o konwersjach na poszczególnych ścieżkach przypomina model liniowy – konwersje rozdzielane są równo pomiędzy wszystkie kanały występujące na ścieżce.
Wartość Shapleya dla liczby konwersji na ścieżkach konwertujących jest swego rodzaju liniowym modelem atrybucji.
Różnica pomiędzy taką Wartością Shapleya a modelem liniowym z Google Analytics polega na tym, że w tym drugim wartość rozdzielana jest po równo każdej z interakcji na ścieżce, a Wartość Shapleya dzieli ją równo pomiędzy kanały. Znaczy to, że jeśli analizujesz wyłącznie ścieżki prowadzące do konwersji, wykorzystanie Wartości Shapleya nie wniesie do analizy wiele więcej, niż standardowe modele heurystyczne.
Wartość Shapleya dla współczynnika konwersji
Sytuacja zacznie wyglądać ciekawiej, gdy za wynik gry uznamy nie liczbę konwersji, ale współczynnik konwersji. Każda kolejna interakcja powinna zwiększać prawdopodobieństwo konwersji, więc modelowo, im dłuższa ścieżka, tym wyższy współczynnik konwersji użytkowników, którzy byli poddani danej kombinacji działań marketingowych.
Do takich obliczeń potrzebne będą informacje nie tylko o ścieżkach, które doprowadziły do konwersji, ale również o interakcjach na ścieżkach niekonwertujących. Takich danych da się pobrać w postaci standardowego raportu Google Analytics. Sposoby na rozwiązanie tego problemu:
- Dane o użytkownikach, którzy mieli interakcje z określonymi kanałami, można uzyskać wykorzystując zaawansowane segmenty użytkowników (warunki i sekwencje);
- Rozwiązaniem może być skorzystanie z alternatywnego systemu śledzenia interakcji, jak np. Campaign Manager (Google Marketing Platform), co pozwoli na kompleksowe śledzenie interakcji, w tym wyświetleń, bez obaw o przekroczenie limitów (co może mieć miejsce w Google Analytics).
Oto nasze przykładowe dane uzupełnione o informacje o liczbie kliknięć i konwersji na wszystkich ścieżkach:
| Ścieżka | Wsp. konw. | Kliknięcia | Konwersje |
|---|---|---|---|
| FB | 2% | 10 000 | 200 |
| G | 5% | 2000 | 100 |
| Aff | 0,2% | 50 000 | 100 |
| FB, G | 6% | 2000 | 120 |
| FB, Aff | 2,5% | 4000 | 100 |
| G, Aff | 6% | 1000 | 60 |
| FB, G, Aff | 8% | 500 | 40 |
| SUMA | 720 |
Do dalszych obliczeń potrzebny będzie przede wszystkim współczynnik konwersji. Obliczmy teraz Wartość Shapleya dla Facebooka. W tym celu – tak samo jak we wcześniejszych przykładach – określamy kombinacje ścieżek zawierające Facebook (FB) i określamy wkład marginalny Facebooka do współczynników konwersji na każdej z tych ścieżek.
Następnie dokonujemy obliczeń zgodnie z formułą Wartości Shapleya:
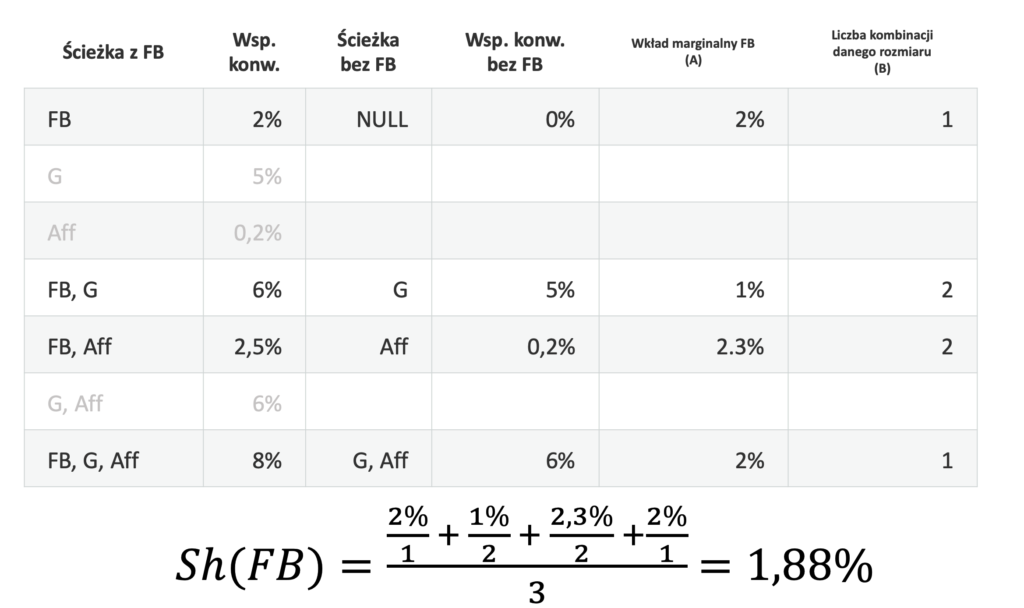
Analogiczne obliczenia wykonujemy dla Google (G):
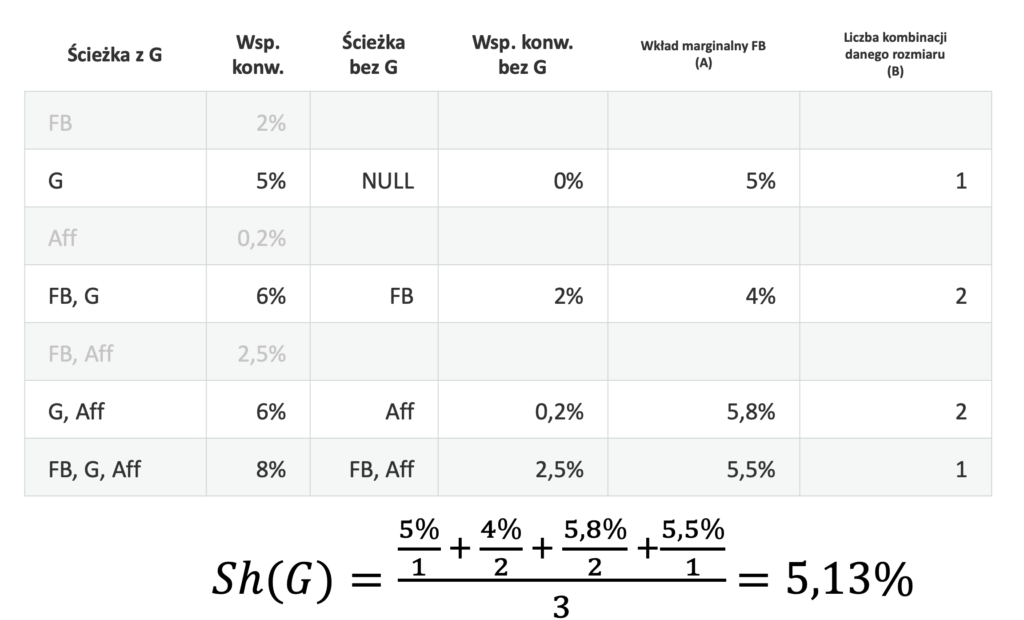
Ponieważ wiemy, że łączny współczynnik konwersji dla wszystkich trzech kanałów wynosi 8%, nie musimy już obliczać formuły Wartości Shapleya dla Afiliacji. Po prostu odejmiemy udziały Facebooka i Google’a od łącznego wyniku:
Sh(Aff) = 8% – Sh(FB) – Sh(FG) = 8% – 1,88% – 5,13% = 0,98%
Mamy więc już wyliczone Wartości Shapleya dla tych źródeł w sytuacji, gdy na ścieżce występują trzy kanały. Z kolei dla ścieżek, na których występuje tylko jeden kanał, rozwiązanie jest trywialne, ich udział jest równy samemu sobie:
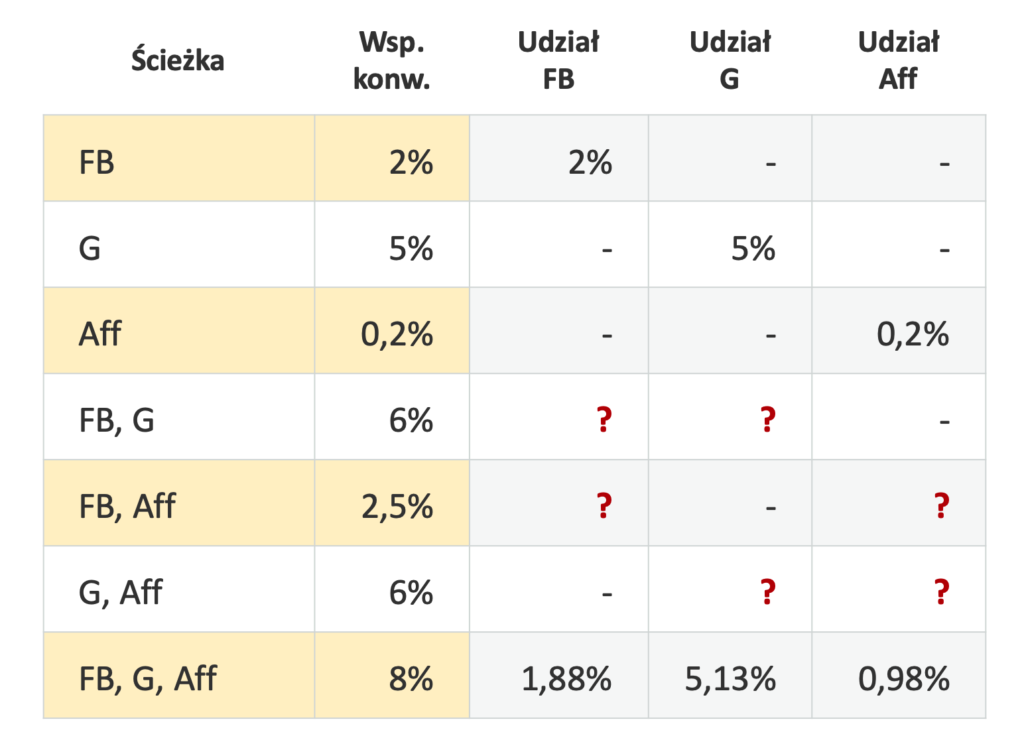
Teraz musimy dokonać takich samych obliczeń dla kombinacji dwóch kanałów. Obliczmy więc Wartość Shapleya dla Facebooka w kombinacji Facebook + Google:
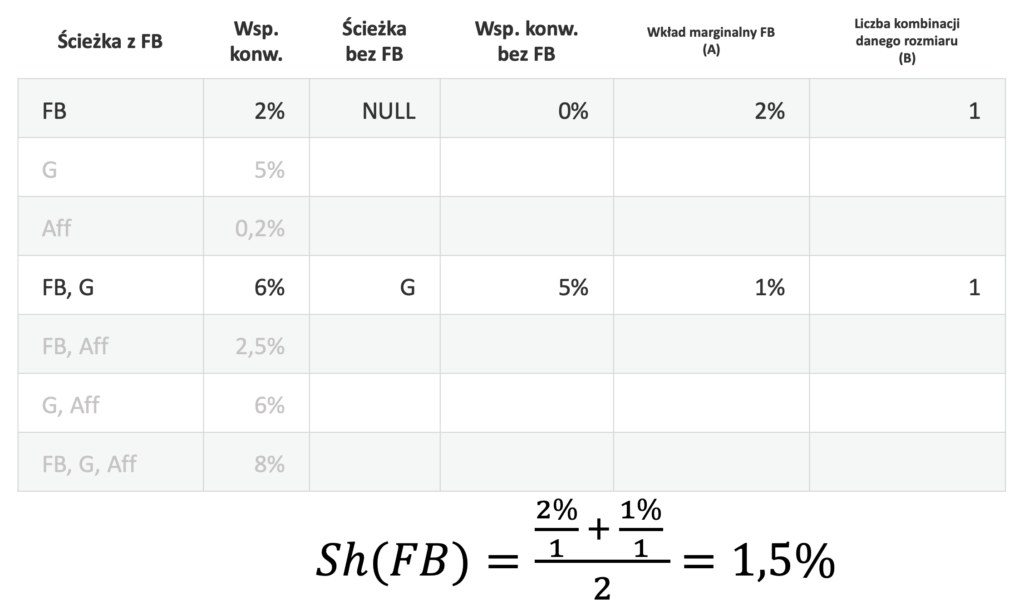
Udział Google będzie różnicą współczynnika konwersji kombinacji Facebook + Google (6%) i Wartości Shapleya dla Facebooka (1,5%):
Sh(G) = 6% – Sh(FB) = 6% – 1,5% = 4,5%
Analogiczne obliczenia pozwolą obliczyć wszystkie Wartości Shapleya dla poszczególnych kombinacji, a następnie obliczyć konwersje, które przypiszemy do poszczególnych kanałów (liczba konwersji = liczba kliknięć × współczynnik konwersji):
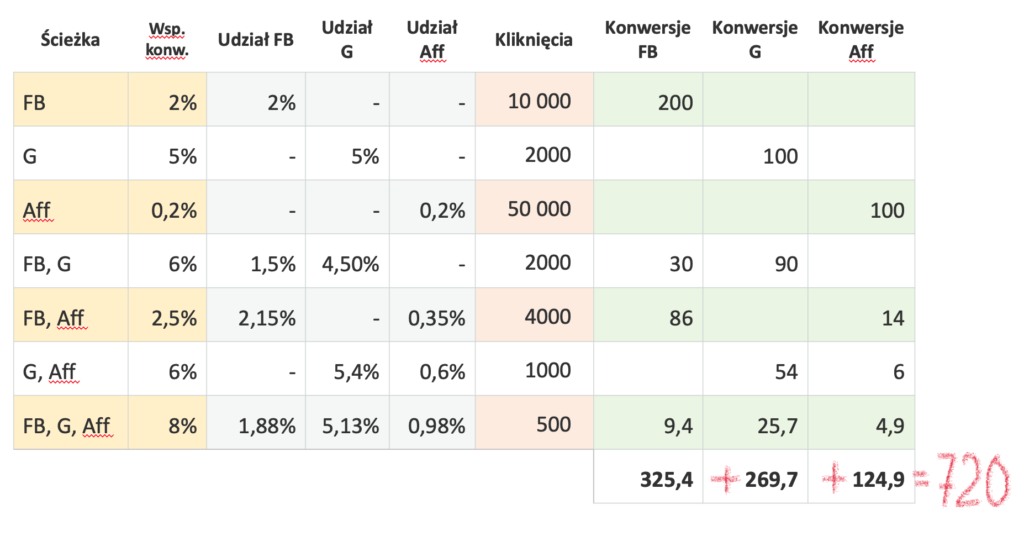
Oczywiście, wartość konwersji przypisanych do poszczególnych źródeł w każdym modelu atrybucji musi się sumować do łącznej liczby wszystkich konwersji (w tym przypadku 720).
W porównaniu z modelem opartym na Wartości Shapleya dla liczby konwersji modelem liniowym, model oparty na Wartości Shapleya dla współczynnika konwersji wykazał istotne różnice:
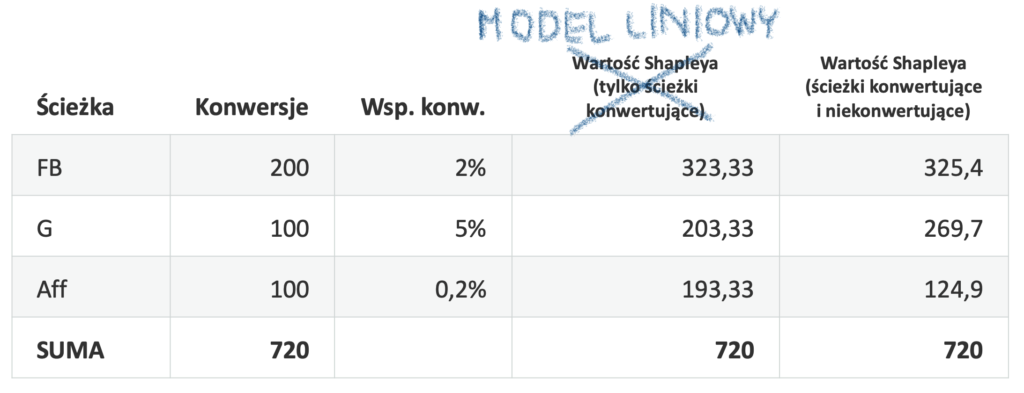
Nastąpiło przesunięcie konwersji z kanału Affiliate do Google, co jest wynikiem premiowania kanałów o wyższym współczynniku konwersji – typowego dla tej implementacji Wartości Shapleya.
Właściwości Wartości Shapleya
Wróćmy na chwilę do definicji Wartości Shapleya. Potrafimy już ją obliczać, ale dlaczego wzór ten jest taki, a nie inny? Jej twórca, laureat Nagrody Nobla Lloyd Shapley, wykazał że jest to jedyna formuła podziału zysku pomiędzy graczy, która spełnia następujące właściwości:
Suma zysków graczy jest równa łącznemu wynikowi. Z punktu widzenia modelowania atrybucji, jest to podstawowy warunek: konwersje przypisane poszczególnym kanałom muszą sumować się do łącznej liczby wszystkich odnotowanych konwersji.
Symetria. Gracze, którzy z punktu widzenia wyniku grają dokładnie taką samą rolę w grze, będą mieli identyczne Wartości Shapleya. Jest to intuicyjny wymóg, jaki stawiamy modelom atrybucji (tę i poprzednią właściwość wykorzystaliśmy już wcześniej przy obliczeniach).
Zerowa wartość gracza nieistotnego. Gracz, który nie wnosi nic do żadnej kombinacji graczy, będzie miał zerową Wartość Shapleya. Kanałom, które nic nie wnoszą, nie przypiszemy żadnej konwersji.
Addytywność. Niezależnie od tego, jak zdefiniujemy wynik danej gry, czyli dla dowolnych funkcji charakterystycznych wynik 1 oraz wynik 2, dla każdego gracza i:
Sh(wynik 1, i) + Sh(wynik 2, i) = Sh (wynik 1 + wynik 2, i)
Przykład. Załóżmy, że mamy klika rodzajów konwersji: transakcja, subskrypcja newslettera i pobranie e-booka. Addytywność oznacza, że suma Wartości Shapleya dla poszczególnych rodzajów konwersji będzie Wartością Shapleya dla konwersji liczonych łącznie. Jeśli więc
konwersje = transakcje + pobrania + subskrypcje
to dla każdego kanału i:
Sh(konwersje, i) = Sh(transakcje, i) + Sh(pobrania, i) + Sh(subskrypcje, i)
Jest to warunek konieczny, by przy segmentacji na poszczególne rodzaje konwersji, wartość transakcji, subskrypcji i pobrań przypisanych dla danego kanału sumowała się do wartości konwersji przypisanych temu kanałowi.
Skoro Wartość Shapleya jest jedyną funkcją, która tę zasadę spełnia, to w zasadzie należałoby uznać, że stanowi idealny model atrybucji. Niestety, ma ona też ograniczenia. Jednym z najczęściej podnoszonych zarzutów jest to, że ignoruje kolejność interakcji. Ścieżki Facebook > Google oraz Google > Facebook czy Google > Facebook > Google > Facebook > Google są sumowane do kombinacji Facebook + Google. Tak więc już na samym początku obróbki danych, zamazujemy informacje, które intuicyjnie wydają się istotne z punktu widzenia analizy.
Ponadto, złożoność obliczeniowa Wartości Shapleya rośnie wykładniczo (2n) wraz z liczbą kanałów biorących udział w procesie konwersji, co znacznie utrudnia jej obliczanie dla większej granulacji kanałów.
Efekt usunięcia
Jedną z intuicyjnych miar wykorzystywanych w modelowaniu atrybucji jest tzw. efekt usunięcia (removal effect), czyli wkład marginalny danego kanału do wszystkich konwersji. Odpowiada na proste pytanie: ile konwersji stracimy, jeśli zrezygnujemy z danej reklamy. Znając efekt usunięcia, możemy prosto to odnieść na decyzję, ile warto zainwestować w daną reklamę by te konwersje odzyskać.
Miara wydaje się prosta, ale ma pewną wadę. Efekty usunięcia zazwyczaj nie sumują się do łącznego efektu. Może się zdarzyć, że wyłączając reklamę w wyszukiwarce, tracisz 80% konwersji, a wyłączając Facebook, będziesz ich mieć o 30% mniej.
Remarketing może zwiększać liczbę konwersji o 1/3 (efekt usunięcia będzie 25%). Po zsumowaniu wychodzi ponad 100%. Alokując budżet na tej podstawie, przydzielilibyśmy więcej, niż mamy do dyspozycji.
Dlatego, aby spełnić podstawową cechę atrybucji, efekty usunięcia są normalizowane tak, aby po zsumowaniu, dały 100%.
| Kanał | Konwersje łączne | Konwersje bez danego kanału | Efekt usunięcia | Efekt usunięcia (znormalizowany) |
|---|---|---|---|---|
| 1000 | 200 | 80% | 53,33% | |
| 1000 | 700 | 30% | 20% | |
| YouTube | 1000 | 850 | 15% | 10% |
| Remarketing | 1000 | 750 | 25% | 16,66% |
| SUMA | 150% | 100% |
Atrybucja na podstawie znormalizowanego efektu usunięcia jest prosta – przypisujemy danemu kanałowi taki procent z wszystkich konwersji, ile wynika z efektu usunięcia. Normalizacja wydaje się rozsądnym rozwiązaniem problemu (jeśli brakuje budżetu, redukuje się go proporcjonalnie).
Niestety, normalizacja powoduje, że w przypadku ścieżek jednokanałowych (takich, na których występuje tylko jedna interakcja), będzie im przypisane mniej konwersji, niż te, w których brały udział. Skoro w konwersji nie brały udziału żadne inne interakcje, to dlaczego dzielimy z nimi udział w konwersji? To przecież bez sensu.
Wartość Shapleya nie ma tego mankamentu.
Mimo tej oczywistej niedoskonałości, efekt usunięcia jest wykorzystywany np. w modelowaniu atrybucji z wykorzystaniem łańcuchów Markowa. Jest nieskomplikowany obliczeniowo i łatwy w bezpośredniej interpretacji, dlatego będziemy go również stosować w dalszych przykładach.
Będzie to wartość obliczana na podstawie współczynników konwersji na ścieżkach, a nie wartość mierzona empirycznie (o tym, że są to dwie różne rzeczy i jak bardzo mogą się różnić, przeczytasz m. in.w artykule na temat eksperymentu conversion lift).
Wartość Shapleya w praktyce
Modele algorytmiczne wprowadzono w nadziei, że na podstawie analizy ścieżek konwersji będą w stanie odczytywać znaczenie danego kanału w generowaniu konwersji, czyli m. in. przewidywać efekt usunięcia danego kanału.
Wartość Shapleya analizuje istniejące ścieżki w ten sposób, że symuluje usunięcie danego kanału. Pozostałe współdziałające z nim kanały pozostają, ale działają już ze współczynnikiem konwersji takim, jak inne takie ścieżki.
Łatwo to zrozumieć na prostym przykładzie. Załóżmy, że mamy dwa źródła, Facebook i Google:
| Kombinacja źródeł | Kliknięcia | Konwersje | Wsp. konw. |
|---|---|---|---|
| 1000 | 50 | 5% | |
| 2000 | 60 | 3% | |
| Facebook + Google | 500 | 30 | 6% |
| SUMA | 3500 | 140 | 4% |
Symulacja usunięcia Google wyglądać będzie tak, że kliknięcia ze ścieżki Facebook + Google pozostaną, ale ich współczynnik będzie taki, jak dla samego Facebooka:
| Kombinacja źródeł | Kliknięcia | Konwersje | Wsp. konw. |
|---|---|---|---|
| Google [usunięte] | 0 | 0 | – |
| 2000 | 60 | 3% | |
| Facebook [potencjalnie z Google] | 500 | 15 | 3% |
| SUMA | 2500 | 75 | 3% |
Click spam
Opisana wyżej własność Wartości Shapleya powoduje, że bardzo dobrze wykrywa click spam, czyli bezwartościowe, przypadkowe interakcje, które mogą się losowo pojawiać na ścieżce konwersji (więcej na ten temat w artykule o nadużyciach w performance marketingu).
Click spam samodzielnie nie generuje żadnych konwersji, a jeśli znajdzie się na ścieżce, nie zwiększa współczynnika konwersji:
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3.00% | |
| 5 000 | 250 | 5.00% | |
| Spam | 20 000 | 0 | 0.00% |
| Facebook, Google | 2 000 | 120 | 6.00% |
| Facebook, Spam | 2 000 | 600 | 3.00% |
| Google, Spam | 15 000 | 750 | 5.00% |
| Facebook, Google, Spam | 10 000 | 600 | 6.00% |
| Total | 82 000 | 2 620 |
Wartość Shapleya dla click spamu będzie wynosić zero, choć praktycznie wszystkie inne modele będą przypisywały spamowi jakąś wartość, mimo że jego efekt usunięcia jest zerowy.
| Shapley Value | Linear | Normalised Removal | |
|---|---|---|---|
| 1 140 | 860 | 1 122.86 | |
| 1 480 | 885 | 1 497.14 | |
| Spam | – | 875 | – |
| TOTAL | 2 620 | 2 620 | 2 620 |
Jest to jedna z najcenniejszych własności Wartości Shapleya.
W praktyce click spam będzie generował jakieś konwersje, ale współczynnik konwersji będzie bardzo niski.
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3.00% | |
| 5 000 | 250 | 5.00% | |
| Spam | 20 000 | 15 | 0.08% |
| Facebook, Google | 2 000 | 120 | 6.00% |
| Facebook, Spam | 20 000 | 600 | 3.00% |
| Google, Spam | 15 000 | 750 | 5.00% |
| Facebook, Google, Spam | 10 000 | 600 | 6.00% |
| Total | 82 000 | 2 635 |
Wartość Shapleya przypisze wtedy te konwersje, które były na jego ścieżce i pewną część konwersji na innych ścieżkach (będzie ona niewielka ze względu na niski współczynnik konwersji click spamu) – mimo że spam nie będzie zwiększał konwersji na innych ścieżkach.
| Shapley Value | Linear | Normalised Removal | Absolute Removal | |
|---|---|---|---|---|
| 1 131.25 | 860 | 1 117.96 | 1 005 | |
| 1 473.13 | 885 | 1 500.35 | 1 348.75 | |
| Spam | 30.63 | 890 | 16.69 | 15. |
| TOTAL | 2 635 | 2 635 | 2 635 | 2368.75 |
Faktycznie, spam nie generuje żadnych konwersji. Jeśli występuje na jakiejś ścieżce jako jedyna interakcja, to tylko dlatego, że na ścieżkach nie widzimy wszystkich interakcji. Przykładowo, ktoś mógł odwiedzić stronę po obejrzeniu reklamy telewizyjnej. Taka interakcja z reklamą TV nie będzie widoczna na ścieżce i dzięki temu click spam zbierze zasługę za tę konwersję.
Rozwiązaniem tego problemu jest modyfikacja danych wejściowych i dodanie niewidocznych interakcji do istniejących ścieżek. Jeśli pojawi się na nich ścieżka reklamy telewizyjnej, click spam ponownie nie będzie samodzielnie generował konwersji, przez co jego Wartość Shapleya spadnie do zera.
Remarketing
Zobaczmy teraz jak Wartość Shapleya zadziała w przypadku remarketingu, który sam nie generuje żadnej konwersji, ale zwiększa o 20% współczynnik konwersji pozostałych ścieżek:
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3.00% | |
| 5 000 | 250 | 5.00% | |
| Remarketing | 0 | 0 | 0.00% |
| Facebook, Google | 2 000 | 120 | 6.00% |
| Facebook, Remarketing | 20 000 | 720 | 3.60% |
| Google, Remarketing | 15 000 | 900 | 6.00% |
| Facebook, Google, Remarketing | 5 000 | 360 | 7.20% |
| Total | 57 000 | 2 650 |
Jak widzimy, Wartość Shapleya dla remarketingu okazała się dwa razy niższa od efektu usunięcia:
| Shapley Value | Linear | Removal Effect | |
|---|---|---|---|
| 1 108.33 | 840 | 1 033.69 | |
| 1 373.33 | 880 | 1 306.21 | |
| Remarketing | 168.33 | 930 | 310.11 |
| TOTAL | 2 650 | 2 650 | 2 650 |
Taki model podziału nie wydaje się być właściwy. Skoro remarketing zwiększył o 20% współczynniki konwersji na ścieżkach, w których brał udział, powinien mu przypadać odpowiedni udział w konwersjach z tych ścieżek. Wartość Shapleya “karze” remarketing za niski współczynnik konwersji (który będzie bardzo niski jeśli zaczniemy uwzględniać wyświetlenia jako interakcje) oraz za fakt, że samodzielnie nie generuje żadnych konwersji.
Zobaczmy, jak by się zmieniły Wartości Shapleya gdyby remarketing przypadkiem wygenerował samodzielną konwersję (niedoskonałość danych wynikająca z okna konwersji lub braku pełnego śledzenia cross-device):
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3.00% | |
| 5 000 | 250 | 5.00% | |
| Remarketing | 100 | 1 | 1.00% |
| Facebook, Google | 2 000 | 120 | 6.00% |
| Facebook, Remarketing | 20 000 | 720 | 3.60% |
| Google, Remarketing | 15 000 | 900 | 6.00% |
| Facebook, Google, Remarketing | 5 000 | 360 | 7.20% |
| Total | 57 100 | 2 651 |
Ta jedna konwersja spowodowała podwojenie (!) Wartości Shapleya dla remarketingu.
| Shapley Value | Linear | Removal Effect | |
|---|---|---|---|
| 1 000 | 840 | 965.56 | |
| 1 290 | 880 | 1 330.33 | |
| Remarketing | 361 | 931 | 355.11 |
| TOTAL | 2 651 | 2 651 | 2 651 |
Zobaczmy jeszcze, co by się stało, gdyby współczynnik konwersji remarketingu okazał się być wysoki w tych nielicznych samodzielnych interakcjach:
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3.00% | |
| 5 000 | 250 | 5.00% | |
| Remarketing | 10 | 1 | 10.00% |
| Facebook, Google | 2 000 | 120 | 6.00% |
| Facebook, Remarketing | 20 000 | 720 | 3.60% |
| Google, Remarketing | 15 000 | 900 | 6.00% |
| Facebook, Google, Remarketing | 5 000 | 360 | 7.20% |
| Total | 57 010 | 2 651 |
W tej sytuacji, Wartość Shapleya przypisałaby remarketingowi większość konwersji:
| Shapley Value | Linear | Removal Effect | |
|---|---|---|---|
| 25 | 840 | 3 513.84 | |
| 540 | 880 | 429.47 | |
| Remarketing | 2 086 | 931 | (1 292.31) |
| TOTAL | 2 651 | 2 651 | 2 651 |
Atrybucja oparta na Wartości Shapleya uznała, że skoro remarketing samodzielnie ma tak wysoki współczynnik konwersji, to pozostałe źródła mają niewielki udział w konwersjach wygenerowanych wspólnie z remarketingiem. Nie widać tego bezpośrednio z tabelek, ale Facebook otrzymał ujemy udział w ścieżkach Facebook + remarketing (Facebook miał udział -1,7%, a remarketing +5,3%, co sumuje się do łącznego wyniku 3,6%).
Removal effect (oparty na współczynnikach konwersjj, a nie badanie empiryczne, takie jak np. conversion lift) dał jeszcze bardziej absurdalne wyniki, co było spowodowane ujemnymi wartościami przypisanymi do Facebooka i Google’a, które po normalizacji wyglądają jak powyżej (nie poddają się żadnej interpretacji).
Dlaczego tak się dzieje? Wartość Shapleya patrzy przede wszystkim na współczynniki konwersji, więc jeśli wśród danych znajdą się przypadkowe, nie mające wiele wspólnego z rzeczywistością odczyty (np. 2 kliknięcia, 1 konwersja, współczynnik konwersji 50%), to dalsze obliczenia będą obciążone poważnymi błędami. Dlatego dane o niskiej istotności statystycznej nie powinny być uwzględniane, bo ich przypadkowe odczyty mogą kompletnie zniszczyć wynik.
Ponadto, Wartość Shapleya uśrednia wkłady marginalne wniesione do poszczególnych kombinacji, więc remarketing, który samodzielnie nic nie generuje, będzie tu uznany za upośledzonego w stosunku do innych źródeł, które samodzielnie są również w stanie generować konwersje. Decyzje budżetowe podejmowane na podstawie takich obliczeń, będą przypuszczalnie krzywdzące dla remarketingu.
Conversion hijacking
Na koniec zobaczmy jak Wartość Shapleya zareaguje na sytuację conversion hijackingu. Są to interakcje sztucznie wstrzykiwane na ścieżkę konwersji tuż przed dokonaniem transakcji, takie jak np. brand bidding czy kupony rabatowe wyszukiwane po przejściu do koszyka (więcej na ten temat w artykule o nadużyciach w performance marketingu).
Przykładem idealnego hijackingu byłoby uznanie za interakcję (touchpoint) kliknięcia w przycisk “zapłać” w koszyku zakupowym – miałyby z nim kontakt wszyscy, którzy dokonali transakcji, a jego współczynnik konwersji byłby niezwykle wysoki.
Hijacking charakteryzuje się tym, że wszystkie ścieżki, na których wystąpi, mają bardzo wysoki współczynnik konwersji, bo są to osoby które za chwilę zamierzają dokonać transakcji. Samodzielnie hijacking nie generuje żadnych konwersji:
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3% | |
| 5 000 | 250 | 5% | |
| Hijack | 0 | 0 | 0% |
| Facebook, Google | 2 000 | 120 | 6% |
| Facebook, Hijack | 1 000 | 100 | 10% |
| Google, Hijack | 500 | 50 | 10% |
| Facebook, Google, Hijack | 200 | 20 | 10% |
| Total | 18 700 | 840 |
Hijacking jest zazwyczaj ostatnią interakcją przed transakcją, dlatego w powyższej sytuacji w modelu last click uzyskałby 170 konwersji. Wartość Shapleya nie dała mu tak dużo, co wynika z faktu, że hijacking nie generuje konwersji samodzielnie, co bardzo obniża jego wynik. Niemniej, wciąż przypisano mu wiele konwersji:
| Shapley Value | Linear | Removal Effect | |
|---|---|---|---|
| 410.67 | 416.67 | 399.55 | |
| 375.17 | 341.67 | 342.47 | |
| Hijack | 54.17 | 81.67 | 97.98 |
| TOTAL | 840 | 840 | 840 |
Zobaczmy, co by się stało gdyby i tutaj pojawiła się choć jedna samodzielna konwersja ze źródła hijackingu:
| Path | Click | Conv. | Conv. rate |
|---|---|---|---|
| 10 000 | 300 | 3% | |
| 5 000 | 250 | 5% | |
| Hijack | 10 | 1 | 10% |
| Facebook, Google | 2 000 | 120 | 6% |
| Facebook, Hijack | 1 000 | 100 | 10% |
| Google, Hijack | 500 | 50 | 10% |
| Facebook, Google, Hijack | 200 | 20 | 10% |
| Total | 18 710 | 841 |
W takiej sytuacji Wartość Shapleya wzrosłaby ponad dwukrotnie:
| Shapley Value | Linear | Removal Effect | Absolute Removal | |
|---|---|---|---|---|
| 357.33 | 416.67 | 366.65 | 320.00 | |
| 346.83 | 341.67 | 355.19 | 310.00 | |
| Hijack | 136.83 | 82.67 | 119.16 | 104.00 |
| TOTAL | 841 | 841 | 841 | 734 |
Wartość Shapleya zareagowała silnie na zaobserwowaną zdolność hijackingu do samodzielnego generowania konwersji (mimo że tylko jednej), a także na wysoki współczynnik konwersji, który w tym przypadku jest wyższy, niż pozostałych źródeł działających samodzielnie. W efekcie, w 170 konwersjach, w których hijacking się pojawił, przypisano mu w udziale aż 136.83 konwersji.
Kalkulator Wartości Shapleya
Do pobrania arkusz umożliwiający obliczanie Wartości Shapleya dla maksymalnie 4 kanałów.
Wartości Shapleya dla 4 kanałów (plik .xlsx)
Podsumowanie
Najważniejsze wnioski z powyższych rozważań:
- Wartość Shapleya jest pewnego rodzaju uśrednieniem wkładów, które dany kanał wnosi do wyniku uzyskiwanego w każdej z kombinacji kanałów.
- Dla wyniku określonego jako liczba konwersji, gdzie brane są pod uwagę tylko ścieżki konwertujące, Wartość Shapleya jest równoważna z modelem liniowym.
- Aby obliczyć Wartość Shapleya dla współczynnika konwersji, potrzebne są również dane o ścieżkach niekonwertujących.
- Wartość Shapleya w ogóle nie bierze pod uwagę kolejności, w jakiej kanały występują na ścieżce.
- Obliczenia co do zasady nie są trudne, ale trzeba je wykonać dla wszystkich kombinacji kanałów, co powoduje, że złożoność obliczeniowa rośnie wykładniczo (2n), więc jej wyliczanie dla dużej liczby kanałów może mocno obciążyć nawet bardzo wydajny komputer.
- W obliczeniach Wartości Shapleya brane są po uwagę przede wszystkim współczynniki konwersji, dlatego miara ta premiuje kanały o wyższych współczynnikach konwersji i mocno ucina te, które samodzielnie nie generują konwersji (takie jak np. remarketing).
- Wartość Shapleya bardzo dobrze wykrywa click spam, jako kanał który nic nie wnosi do współczynnika konwersji żadnej ze ścieżek. Prawidłowo interpretuje również ścieżki jednokanałowe (nie dzieli wygenerowanych przez nie konwersji z innymi kanałami).
- Wartość Shapleya jest bardzo wrażliwa na przypadkowe wartości o niewielkiej istotności statystycznej, które traktuje na równi z wiarygodnymi danymi. Dlatego do jej obliczania należy stosować wyłącznie dane o odpowiednim wolumenie konwersji, dla których odczyt współczynnika konwersji jest obarczony niewielkim błędem statystycznym.
- W połączeniu z faktem, że obliczenia dużej liczby kanałów będą bardzo zasobochłonne, można stwierdzić, że Wartość Shapleya najlepiej obliczać dla interakcji pogrupowanych w niewielką liczbę kanałów, z których każdy zawiera dane o odpowiedniej istotności statystycznej.
Wartość Shapleya jest zasilana danymi o wkładach marginalnych wyliczanych z obserwowanych współczynników konwersji na ścieżkach. Nie jest to pomiar empiryczny. Jest to jeden z powodów, dla których nie interpretuje prawidłowo wkładów wnoszonych przez interakcje typu conversion hijacking.
Alternatywą do Wartości Shapleya są modele wykorzystujące łańcuchy Markowa.
W artykule tym terminologia matematyczna została celowo uproszczona dla ułatwienia zrozumienia istoty opisywanego zagadnienia.
Następny artykuł (cz. 11): Łańcuchy Markowa
Warto przeczytać: Przewodnik po atrybucji w Google Analytics


