Profit-driven optimization and the ROI>1/E model indicates that applying a uniform target ROI for the entire campaign is not optimal, and it should be adjusted according to the price elasticity occurring in different dimensions.
See the article about profit-driven optimization and the ROI>1/E model.
Applying the ROI>1/E model is not always possible. One of the main reasons is the precise determination of the conversion value, taking into account the Lifetime Value. Another typical situation is limitations related to the budgetary rigor of the campaign and the ability to finance long-term investments.
An example could be an advertiser who needs to fund campaigns from current income, for whom the optimization goal is to maximize revenue growth while maintaining a short-term ROI at certain level.
In such a situation, the profitability parameter (ROI) is predetermined, and profit-driven optimization boils down to maximizing conversion value within the set profitability.
Naive Optimization
When optimizing marketing campaigns, marketers often try to pursue the same goal across all channels and campaigns. In the case of a goal such as ROI = 0, it would be maintained in all campaigns.
Optimization would mean that maximum CPC bids for keywords where the assumed cost per conversion is exceeded are lowered, while where the assumed cost per conversion is not yet reached, there is room for raising bids and improving campaign efficiency.
However, we know that due to differences in the elasticity of individual channels, campaigns, and other elements for which we can set bids, this will not be optimal.
Relationship Between Marginal Cost and Elasticity
Elasticity is defined as the ratio of the relative increase in campaign effect (clicks, conversions, or revenue) to the relative increase in unit cost (respectively CPC, CPA, or ERS – Effective Revenue Share = 1/ROAS).
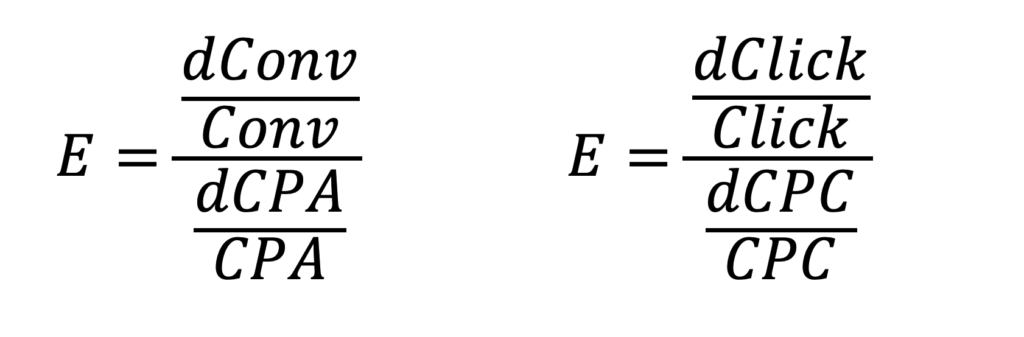
By transforming the formula derived from this definition, we obtain the relationship between elasticity and marginal unit cost:
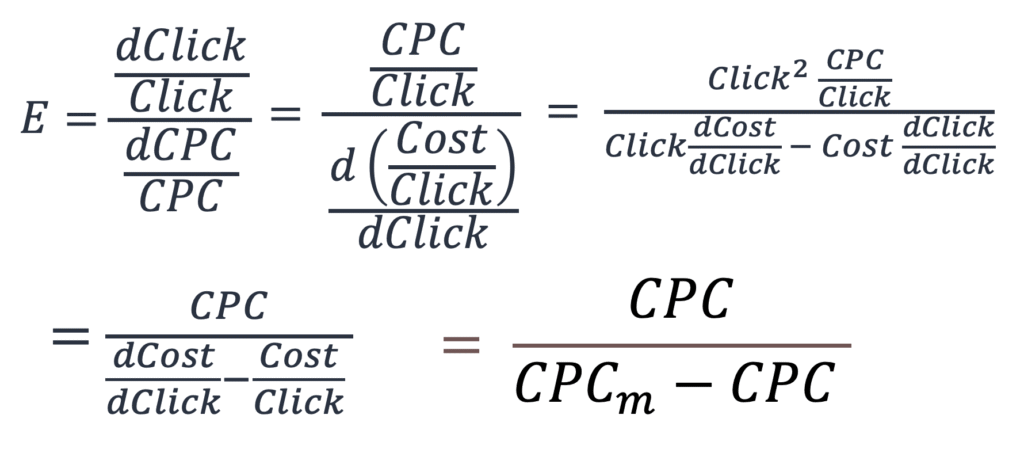
Which can be further transformed into:
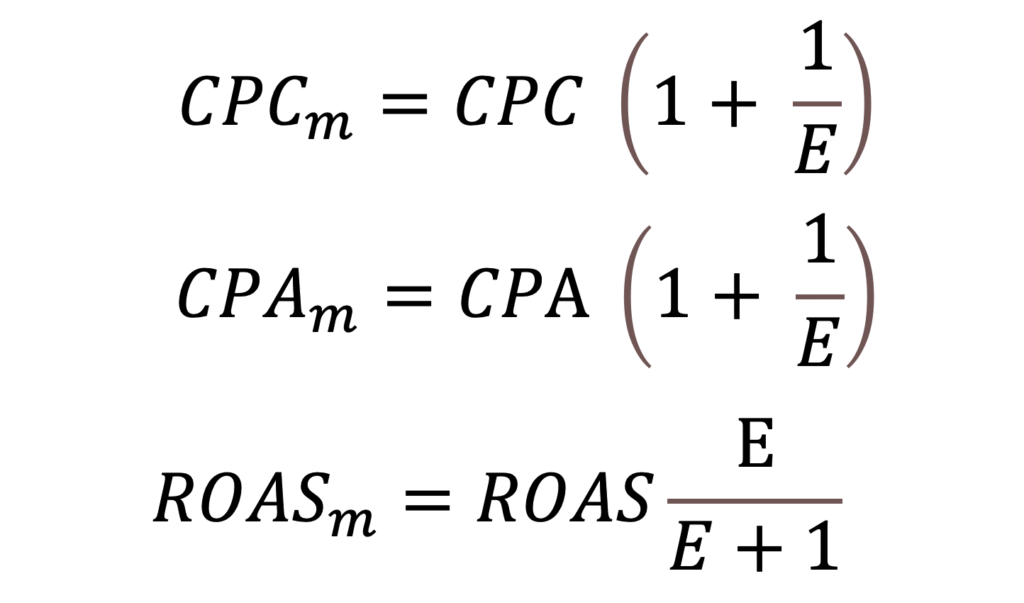
Portfolio Balance
Shifting budget from one campaign to another makes sense when we transfer budget from a campaign with a higher marginal cost to a campaign with a lower marginal cost.
For example, if in Campaign A the marginal cost per conversion (CPA) is $15, and in Campaign B the marginal CPA is $10, then by reducing Campaign A’s budget by $15 we lose one conversion, but by increasing Campaign B’s budget by $10 we gain one conversion. After such an operation, the total number of conversions remains the same, and we have saved $5, which can be used to acquire additional conversions.
The equilibrium point is therefore when all campaigns have the same marginal profitability (and not the same overall profitability – due to differences in elasticity, the ratio of total to marginal profitability will vary).
Adjusting for Elasticity
What adjustments compared to “classic,” naive optimization will this involve?
Assume a campaign consisting of two parts (e.g., two ad groups or two keywords) achieves the target ROI for each of these parts. We want to change the target CPC in these two parts to achieve the highest possible increase in sales (conversion value) while maintaining target ROI.
Adjustment calculation
Two parts of the campaign perform at certain ROI. We want to change the bids and maximally increase the conversion value, without changing the average ROI.
The growth (G) of the total conversion value after the change is:

– where V is the value of click and Clk is the number of clicks.
Before the changes all parts of the campaign have the same ROI. Therefore:

After the changes, the average ROI remains unchanged i.e. the total value of clicks is equal to the total cost multiplied by (ROI+1):

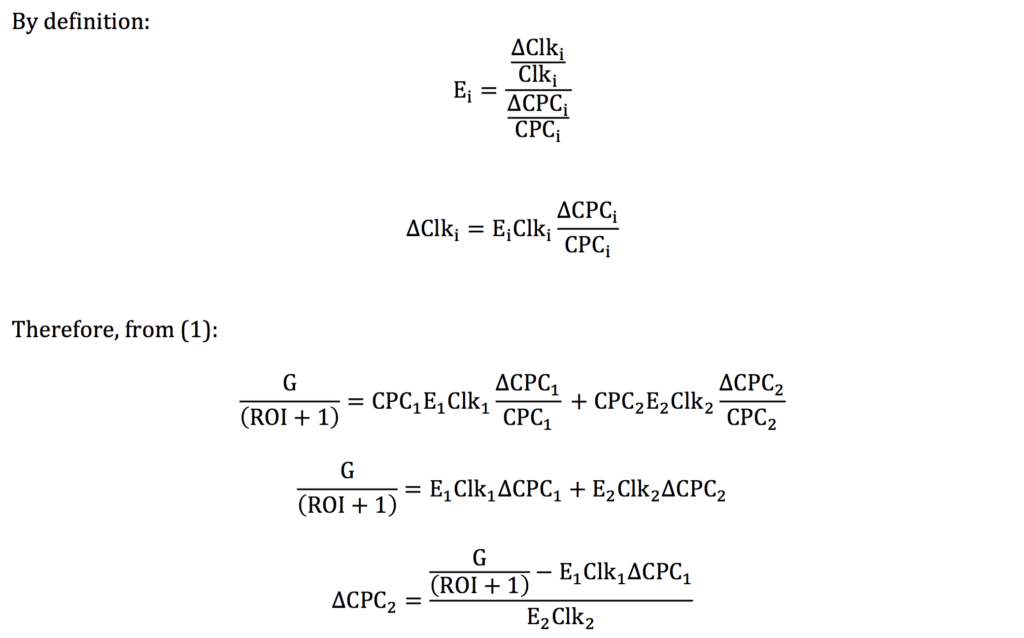
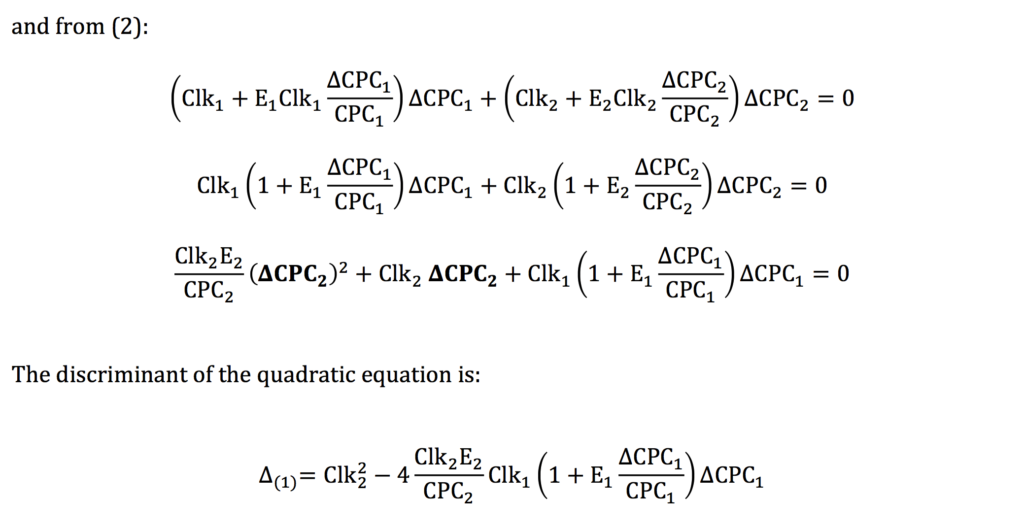
At the maximum growth (G):

The discriminant of the quadratic equation is:
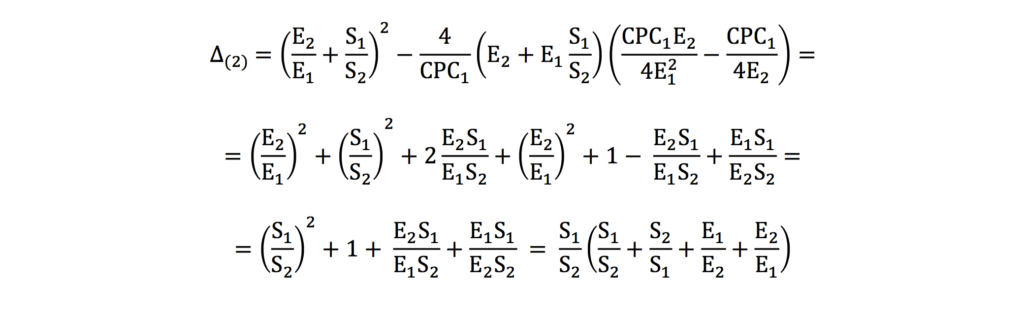
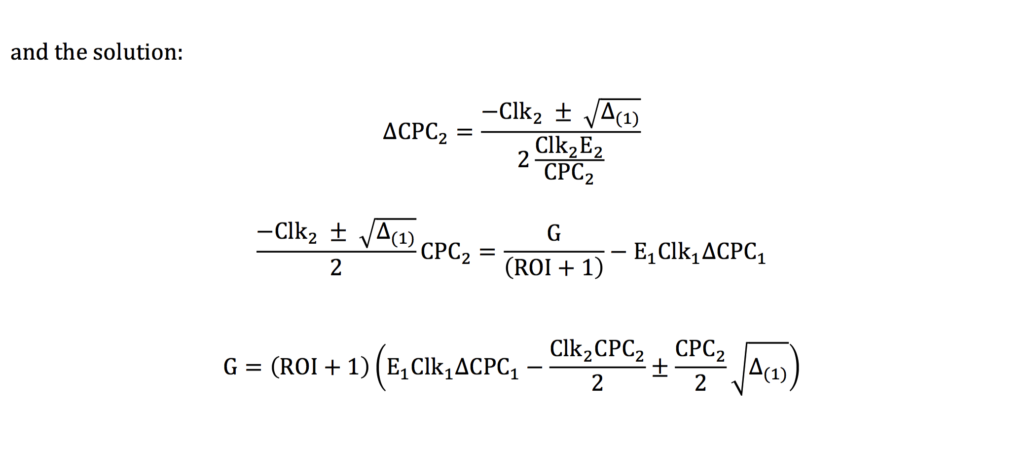
and the solution:


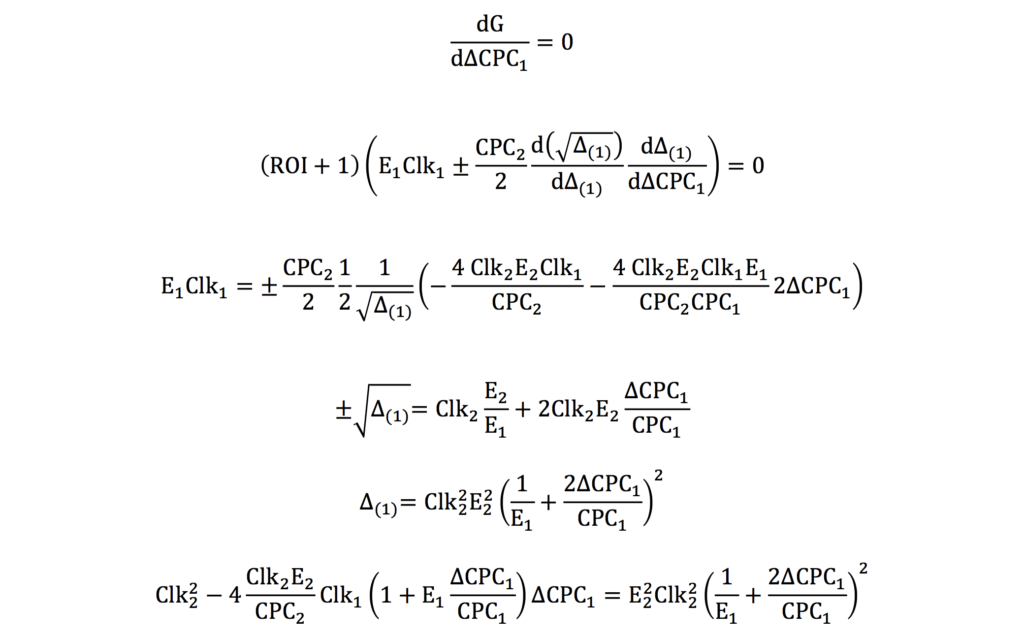
Changing CPC by ΔCPC will maximise the income without changing the total ROI:

The elasticity data are available in Google Ads interface (Bid Simulator) or via API (Bid Landscapes). The “1” and “2” may be any part/segment of the campaign: keyword, adgroup, segment. For example, “1” can be “mobile” and “2” – “desktop”, or “1” can be a keyword and “2” – all the other keywords in the campaign (in this case we should calculate total elasticity of all the other keywords).
How to calculate total elasticity of two campaigns?
From definition:
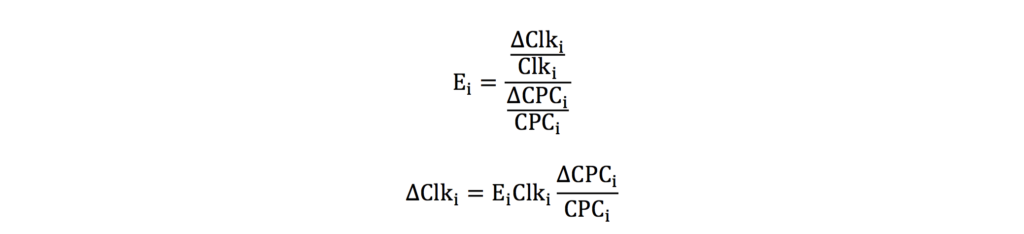
If in all campaigns the relative change of CPC is the same:
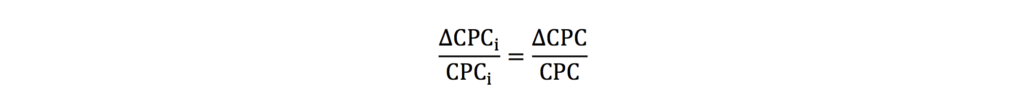
The formula for total elasticity is:

This model assumes that price elasticity does not change within the range of changes in campaigns. However, in reality, price elasticity decreases as CPC increase.
Therefore significant changes of bids may be inaccurate and sometimes may have no meaning (e.g. change of bid below minus 100%).
In practice, if the formula implies very significant changes of bids, you should not modify bids more than by 20-25% and after this modification, measure the elasticity again and continue optimisation at the next iteration.


