PPC campaigns are usually optimised towards unified profitability goals, such as target cost per conversion or ROAS (Return On Advertising Spending) in order to achieve specific ROI (Return on Investment). But does it really maximise the performance?
The formula of ROI, normally used for financial investment profitability analysis, is not optimal for analysing advertising campaigns. The ultimate goal of e-commerce businesses is to maximise profit, not ROI or cost per conversion. Only marginal profit analysis makes it possible to find the optimal level of advertising campaigns.
The formula described in this article makes marginal profit optimisation relatively easy to enforce in campaign management practice: The bids in the campaign should be increased if the current ROI is greater than the reciprocal of the current price elasticity of clicks. Otherwise, the bids should be decreased.
Marginal profit and cost per conversion
An advertiser, who sells their product online, gains $20 profit per transaction (conversion). The advertiser sets a goal of target cost per conversion of, say, $15 for the PPC campaign.
The campaign brings 1000 conversions spending $12,000 monthly, i.e. the cost per conversion is equal to $12. The advertiser decides therefore to increase the bids and gain more traffic from this campaign. As result of higher bids, the campaign brings 1300 conversions, spending $19,500, i.e. the cost per conversion raises to $15. The revenue grows, and the cost per conversion is at the target.
Was the decision to increase the campaign correct? Let’s calculate the cost of additional conversions: Due to increased bids, the campaign acquired 300 more conversions, and its cost increased by $7,500. This means that the additional 300 conversions were acquired at cost of $25 per conversion, and each additional conversion brought $5 loss. The marginal ROI is negative in this case (-20%) and the profit decreases by $1,500.
| Conv. | Revenue | Cost | Profit | ROI | Cost per conv. | |
|---|---|---|---|---|---|---|
| Optimum campaign | 1000 | $20,000 | $12,000 | $8,000 | 66.7% | $12 |
| Aggressive campaign | 1300 | $26,000 | $19,500 | $6,500 | 33.3% | $15 |
| Change / marginal value | +300 | +$6,000 | +$7,500 | -$1,500 | -20.0% | $25 |
This example shows why cost per conversion is not the optimal target for e-commerce campaigns.
ROI of the PCC campaigns normally decreases if the bids, clicks and number of conversions increase; therefore maximisation of ROI usually leads to a significant limitation of the campaign. However, the example campaign after the changes still has a positive ROI = 33.3%, but the marginal ROI is negative (-20%).
The bids should be increased as long as the profit grows, and the optimum point of the campaign is where the marginal profit (or ROI) is equal to zero.
The marginal ERS
Marginal profit analysis may look complex, especially in day-to-day campaign management. However, a simple formula can help us to find the optimal point using KPI available in typical campaign statistics.
We are looking for an indicator, showing when the increase of bids will not only increase CPC and clicks, but also increase our profit.
The increase of bids is profitable as long as the additional investment higher additional conversion value than the additional money spent. In other words, it makes sense as long as the marginal cost is lower than marginal revenue.
The Effective Revenue Share (ERS) is defined as:
ERS = Cost / R
were R is the revenue (conversions value). If ERS = 1, cost is equal to the revenue and the profit is equal to zero.
The additional investment will increase profit only if the marginal ERS is lower than 1:
ERSm < 1
The elasticity of the marketing campaigns indicates how strong will be the relative growth of revenue in comparison to the relative increase of the unit ad price, such as ERS:

A short calculation shows that:
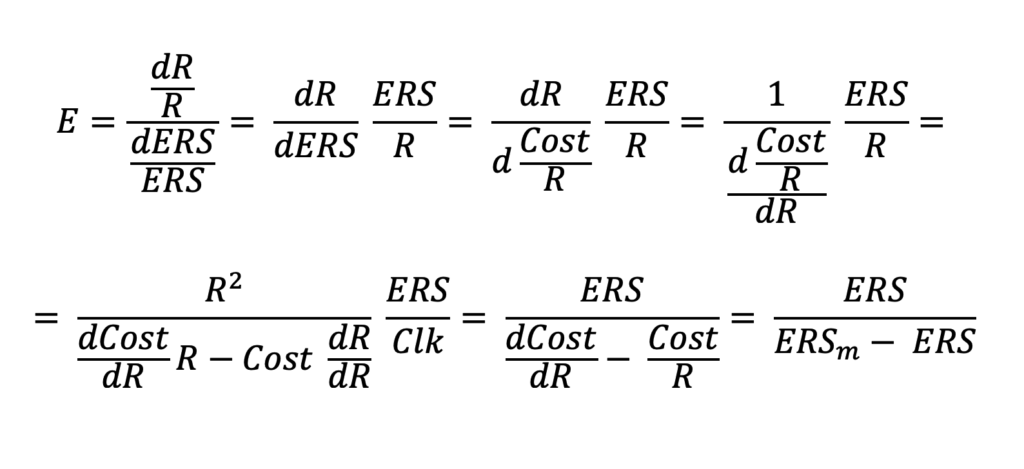
Therefore, the marginal ERS can be calculated as:
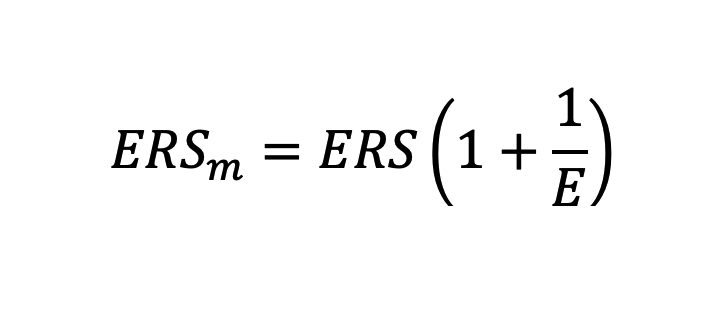
Therefore, the marginal ERS lower than 1 (and the additional investment is profitable) if:
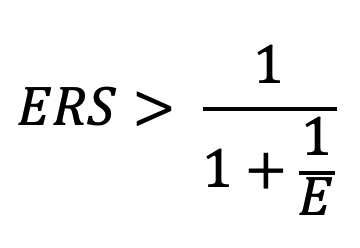
By definition, ERS = 1 / ROAS and ROI = ROAS – 1. Therefore, this condition can be also written
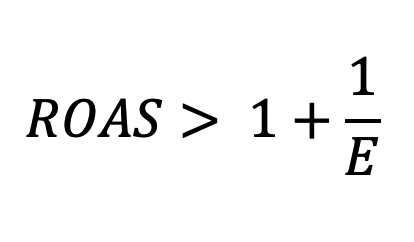
or
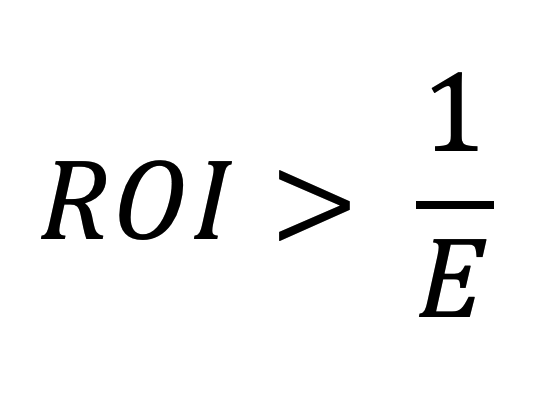
Following the calculations, we have arrived at a relatively simple inequality.
The interplay between Elasticity and key performance indicators such ROAS (or ROI or ERS) is the fundamental determinant of the profitability of incremental investments in marketing campaigns.
The meaning of elasticity
Although ROI, ROAS, and ERS are widely recognised KPIs in marketing, Elasticity is less immediately graspable.
The aforementioned definition characterises elasticity in terms of the relationship between revenue and ERS. However, we can assume that
- the revenue per conversion remains constant, i.e. the clients generated by the additional investment will have the same average shopping basket value, and
- the conversion rate does not change, i.e. the additional traffic purchased will be of the same quality
Under these conditions, we can articulate Elasticity as the relationship between the volume of traffic (measured in the number of clicks) and its unit cost (Cost Per Click, CPC):
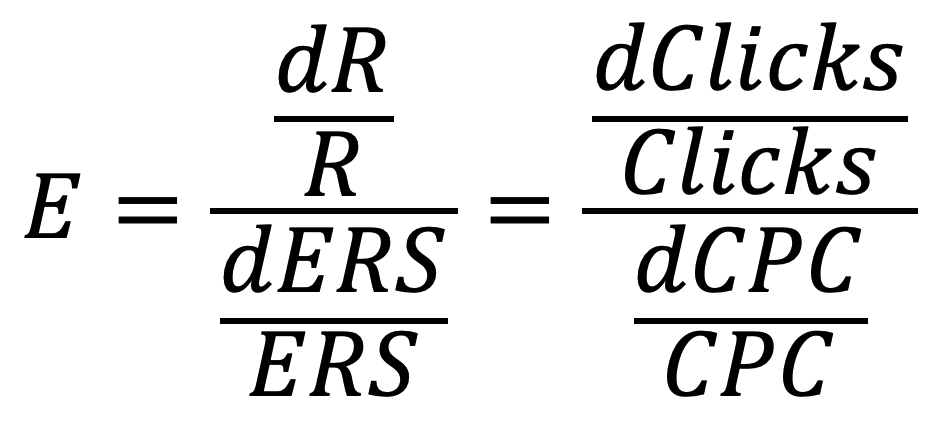
Elasticity reflects the rate at which traffic accelerates in response to higher bidding by advertisers, leading to an increase in the Cost Per Click. It is defined as the relative growth of traffic in proportion to the relative increase in the CPC.
The following table provides an illustrative example of how elasticity can be determined by the CPC and traffic volume (clicks) before and after additional investment in the campaign:
| Before | After | Change | Relative Change | |
|---|---|---|---|---|
| CPC | $10 | $11 | $1 | 10% |
| Clicks | 1000 | 1200 | 200 | 20% |
However, in the current era of using smart bidding strategies such as target ROAS, rather than manual CPC bids, the revenue generated becomes the result of the campaign and ROAS or ERS serve as the metrics in which the cost of traffic is denominated.
The law of diminishing returns
In today’s auction-based marketing systems, advertisers seeking to acquire more clicks must raise their bids. This increase is necessary to outperform competitors who are also aiming to reach the same audience and advertise in similar placements.
The relation of Clicks and CPC is a non-linear function. Generally, this function is increasing (the more clicks, the higher CPC) and usually concave (the more clicks, the faster CPC grows). In the limit, higher CPC does not increase the number of clicks anymore.
An example chart of Click(CPC) function is shown below:
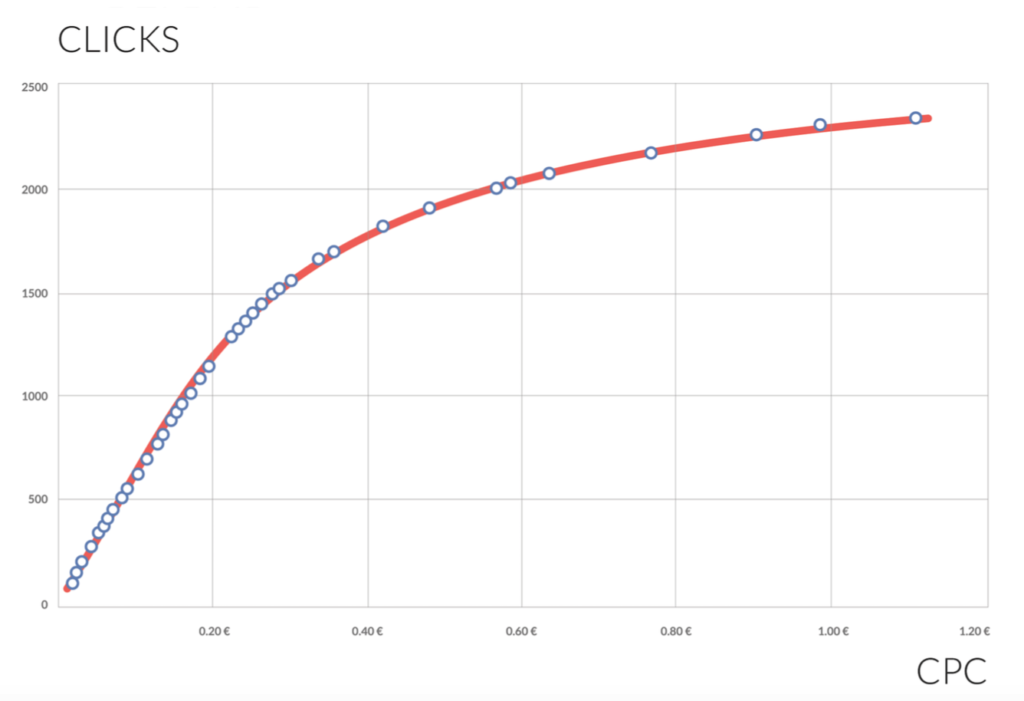
After conversion to price elasticity function, we observe that the elasticity decreases.
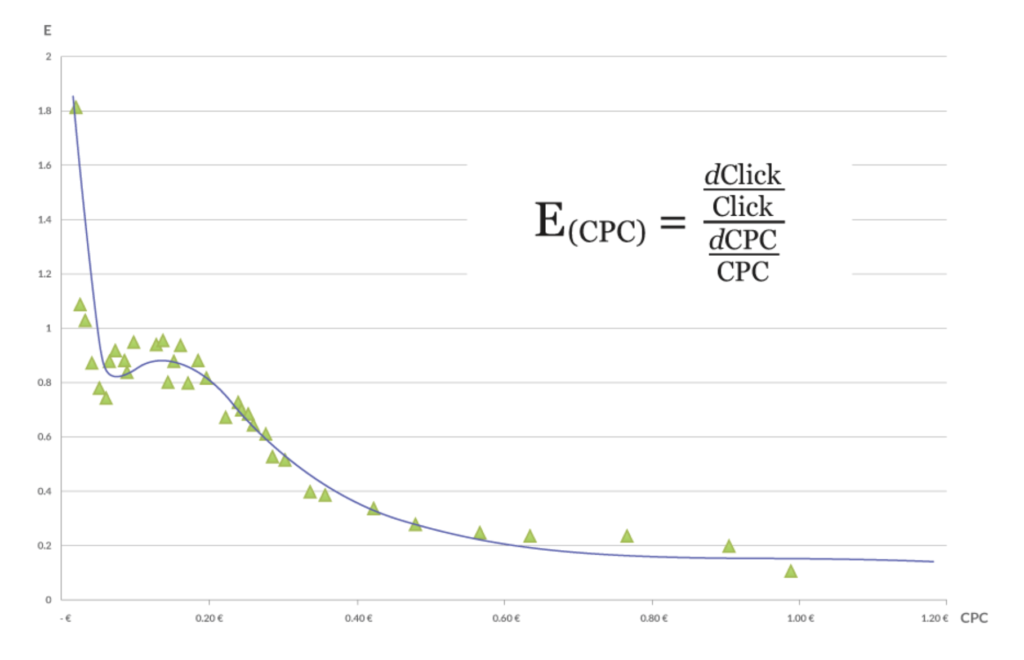
It’s the manifestation of the law of diminishing returns and a consequence of the fact that each resource is limited.
Practical use
In Google Ads, the elasticity can be determined by the bid simulator data
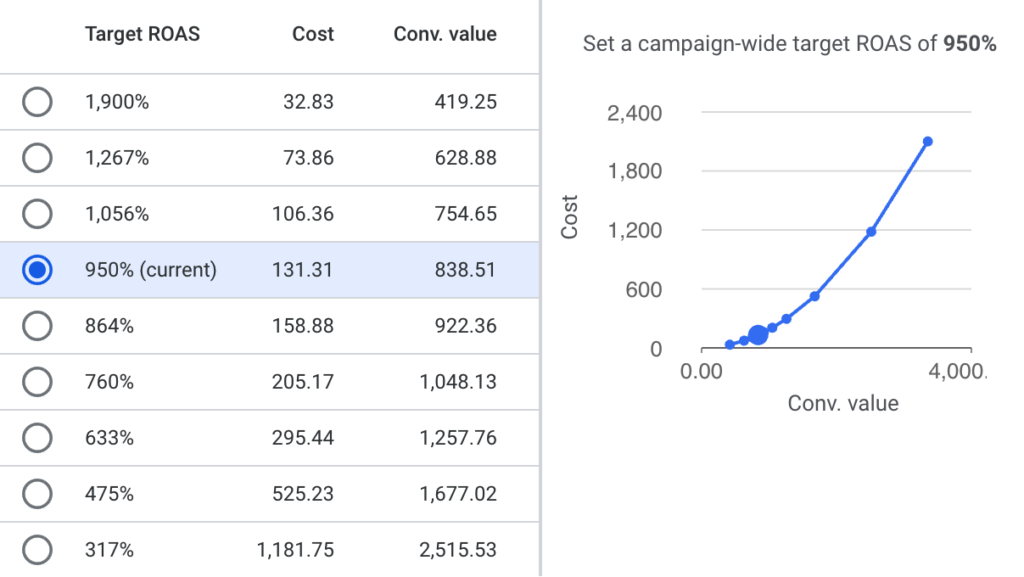
or the performance planner estimations:
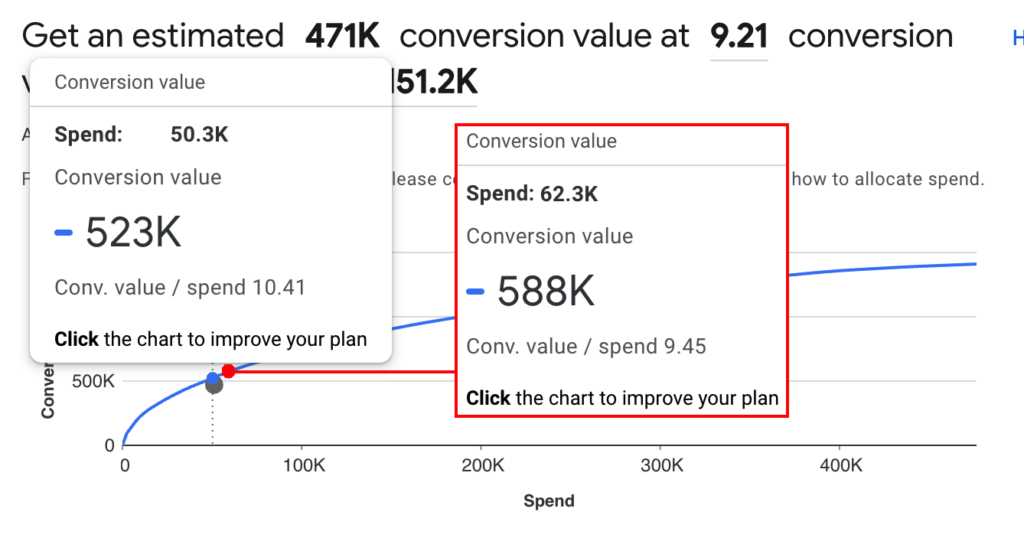
In the example above, more aggressive bidding will result in change of the conversion value (revenue) from 523K to 588K (+12,4%) while the ERS changes from 50.3/523 = 0,0961 to 62.3/588 = 0,1062, i.e the relative growth is 0.1062/0.0961 – 1 = 10,5%. Therefore, the current elasticity is 12,4%/10,5% = 1,18.
The reported ROAS of the campaign is currently 10.41. However, ROAS in ecommerce is usually reported to the revenue which is not equal to the margin, because it includes cost of goods sold (COGS) and sometimes also taxes like Value Added Tax. Therefore in order to calculate the actual net revenue, the ROAS reported should be multiplied by the net margin rate and divided by (1 + tax rate) if applicable.
For example, if the Net Margin = (Net Revenue – Net COGS) / (Net Revenue) = 30%, and the tax rate is 20%, the actual ROAStrue of the campaign should is 10.41 x 30% / (1 + 20%) = 2.60.
If we would like to use the ROAS > (1 + 1/E) formula, we can see that the 1 + 1/E = 1.84, which is significantly less than the current ROAStrue = 2.60.
It means that the campaign is underinvested and the increase of the investment (which will require decreasing the target ROAS) should be profitable.
Between underinvestment and overinvestment
Additional investment in marketing campaign will likely increase the revenue, but it usually will result in lower ROI. The profit can either increase or decrease, depending on the current ROI and elasticity of the marketing campaign. If the ROI > 1/E is no longer true, we have invested too much.
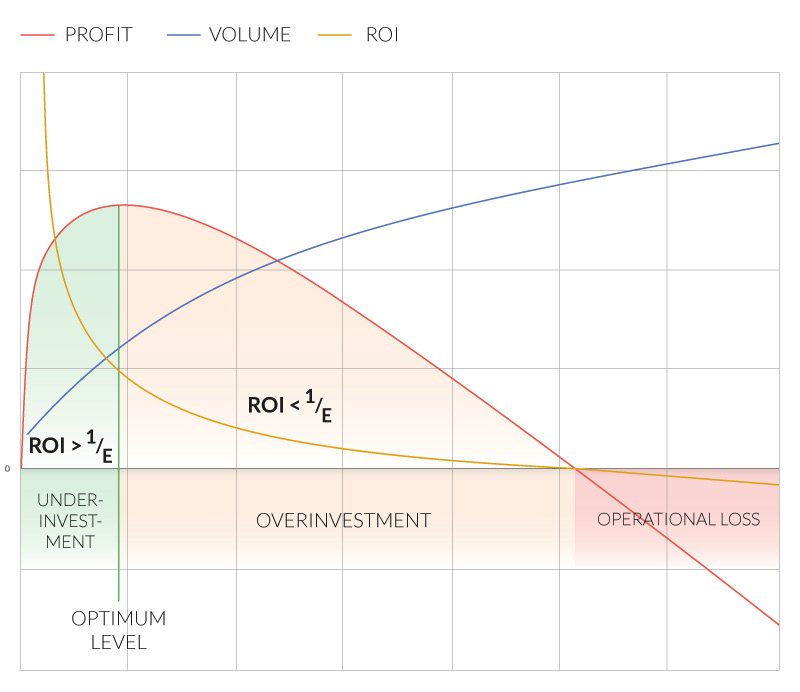
The analysis of marginal profit is the most accurate method of campaign optimisation and brings better results than target cost per conversion or target ROI. The presented formula makes marginal profit analysis relatively easy: the bids in the campaign should be increased if the current ROI is greater than the reciprocal of the current price elasticity of clicks. Otherwise, the bids should be decreased.
See also the article on portfolio bidding strategies.
ⓒ 2015-2024 Adequate Ineractive Boutique


